12  Evaluating Classification Models

Settling In

  • Sit with your NEW group from last class. If anyone in your group wasn’t here, please re-introduce yourselves!
  • Locate and open today’s QMD
  • Catch up on announcements/messages on Slack
  • Hand in your Quiz 1 Revisions

Learning Goals

  • Calculate (by hand from confusion matrices) and contextually interpret overall accuracy, sensitivity, and specificity
  • Construct and interpret plots of predicted probabilities across classes
  • Explain how a ROC curve is constructed and the rationale behind AUC as an evaluation metric
  • Appropriately use and interpret the no-information rate to evaluate accuracy metrics

Notes: Classification Evaluation

Where are we?

CONTEXT

  • world = supervised learning
    We want to model some output variable \(y\) using a set of potential predictors (\(x_1, x_2, ..., x_p\)).

  • task = CLASSIFICATION
    \(y\) is categorical and binary

  • (parametric) algorithm
    logistic regression

  • application = classification

    • Use our algorithm to calculate the probability that y = 1.
    • Turn these into binary classifications using a classification rule. For some probability threshold c:
      • If the probability that y = 1 is at least c, classify y as 1.
      • Otherwise, classify y as 0.
    • WE get to pick c. This should be guided by context (what are the consequences of misclassification?) and the quality of the resulting classifications.


GOAL

  • Evaluate the quality of binary classifications of \(y\) (here resulting logistic regression model).





Sensitivity & specificity

\[\begin{split} \text{overall accuracy} & = \text{probability of making a correct classification} \\ \text{sensitivity} & = \text{true positive rate}\\ & = \text{probability of correctly classifying $y=1$ as $y=1$} \\ \text{specificity} & = \text{true negative rate} \\ & = \text{probability of correctly classifying $y=0$ as $y=0$} \\ \text{1 - specificity} & = \text{false positive rate} \\ & = \text{probability of classifying $y=0$ as $y=1$} \\ \end{split}\]

. . .


In-sample estimation (how well our model classifies the same data points we used to build it)

y = 0 y = 1
classify as 0 a b
classify as 1 c d

\[\begin{split} \text{overall accuracy} & = \frac{a + d}{a + b + c + d}\\ \text{sensitivity} & = \frac{d}{b + d} \\ \text{specificity} & = \frac{a}{a + c} \\ \end{split}\]

. . .


k-Fold Cross-Validation (how well our model classifies NEW data points)

  • Divide the data into k folds of approximately equal size.
  • Repeat the following procedures for each fold j = 1, 2, …, k:
    • Remove fold j from the data set.
    • Fit a model using the other k - 1 folds.
    • Use this model to classify the outcomes for the data points in fold j.
    • Calculate the overall accuracy, sensitivity, and specificity of these classifications.
  • Average the metrics across the k folds. This gives our CV estimates of overall accuracy, sensitivity, and specificity.







ROC curves

ROC: Receiver Operating Characteristic curves

. . .

Sensitivity and specificity depend upon the specific probability threshold c.

  • If we lower c, hence make it easier to classify y as 1:
    • sensitivity increases but specificity decreases
  • If we increase c, hence make it tougher to classify y as 1:
    • specificity increases but sensitivity decreases

. . .

To understand this trade-off, for a range of possible thresholds c between 0 and 1, ROC curves calculate and plot

  • y-axis: sensitivity (true positive rate)
  • x-axis: 1 - specificity (false positive rate)
    • Since specificity is the probability of classifying y = 0 as 0, 1 - specificity is the probability of misclassifying y = 0 as 1.

. . .

Why we care:

  • Along with context, ROC curves can help us identify an appropriate probability threshold c.
  • ROC curves can help us compare the quality of different models.
  • The area under an ROC curve (AUC) estimates the probability that our algorithm is more likely to classify y = 1 as 1 than to classify y = 0 as 1, hence distinguish between the 2 classes.
    • Put another way: if we give our model 2 data points, one with y = 0 and the other with y = 1, AUC is the probability that we correctly identify which is which.







Small Group Discussion

Open the QMD template for today.

Example 1

Suppose we model RainTomorrow in Sydney using only the number of hours of bright Sunshine today.

Using a probability threshold of 0.5, this model produces the following classification rule:

  • If Sunshine < 3.125, predict rain.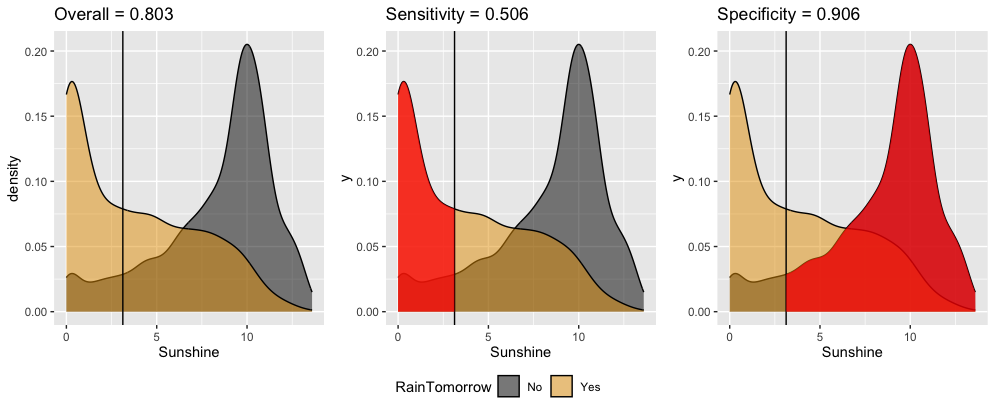
  • Otherwise, predict no rain.

Interpret these in-sample estimates of the resulting classification quality.

  1. Overall accuracy = 0.803
    • We correctly predict the rain outcome (yes or no) 80.3% of the time.
    • We correctly predict “no rain” on 80.3% of non-rainy days.
    • We correctly predict “rain” on 80.3% of rainy days.
  2. Sensitivity = 0.506
    • We correctly predict the rain outcome (yes or no) 50.6% of the time.
    • We correctly predict “no rain” on 50.6% of non-rainy days.
    • We correctly predict “rain” on 50.6% of rainy days.
  3. Specificity = 0.906
    • We correctly predict the rain outcome (yes or no) 90.6% of the time.
    • We correctly predict “no rain” on 90.6% of non-rainy days.
    • We correctly predict “rain” on 90.6% of rainy days.
Solution:
  1. Overall accuracy = 0.803; We correctly predict the rain outcome (yes or no) 80.3% of the time.
  2. Sensitivity = 0.506; We correctly predict “rain” on 50.6% of rainy days.
  3. Specificity = 0.906; We correctly predict “no rain” on 90.6% of non-rainy days.

(OPTIONAL) Extra Practice

Confirm the 3 metrics above using the confusion matrix. Work is shown below (peek when you’re ready).

            Truth
Prediction   No  Yes
       No  3108  588
       Yes  324  602
Solution: 
# Overall accuracy
(3108 + 602) / (3108 + 602 + 324 + 588)
[1] 0.8026828
# Sensitivity
602 / (602 + 588)
[1] 0.5058824
# Specificity
3108 / (3108 + 324)
[1] 0.9055944

Example 2: ROC curves

We can change up the probability threshold in our classification rule!

The ROC curve for our logistic regression model of RainTomorrow by Sunshine plots the sensitivity (true positive rate) vs 1 - specificity (false positive rate) corresponding to “every” possible threshold:

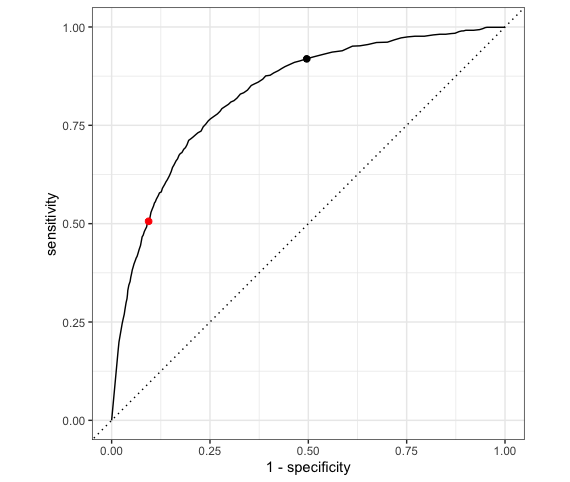
  1. Which point represents the quality of our classification rule using a 0.5 probability threshold?

  2. The other point corresponds to a different classification rule which uses a different threshold. Is that threshold smaller or bigger than 0.5?

  3. Which classification rule do you prefer?

Solution:
  1. Red point: 0.5 probability rule (sensitivity ~ 0.5, specificity ~ 0.9)
  2. Black point (higher sensitivity, lower specificity) has a threshold that is lower than 0.5.
  3. Answers will vary. If you don’t like getting wet (accurately predict rain when it does rain), you’ll want a higher sensitivity. If you don’t like carrying an umbrella when it isn’t needed, you’ll want a higher specificity (lower false positive rate).

Example 3: Area Under the ROC Curve (AUC)

The area under an ROC curve (AUC) estimates the probability that our algorithm is more likely to classify y = 1 (rain) as 1 (rain) than to classify y = 0 (no rain) as 1 (rain), hence distinguish between the 2 classes.

AUC is helpful for evaluating and comparing the overall quality of classification models. Consider 3 different possible predictors (A, B, C) of rainy and non-rainy days:

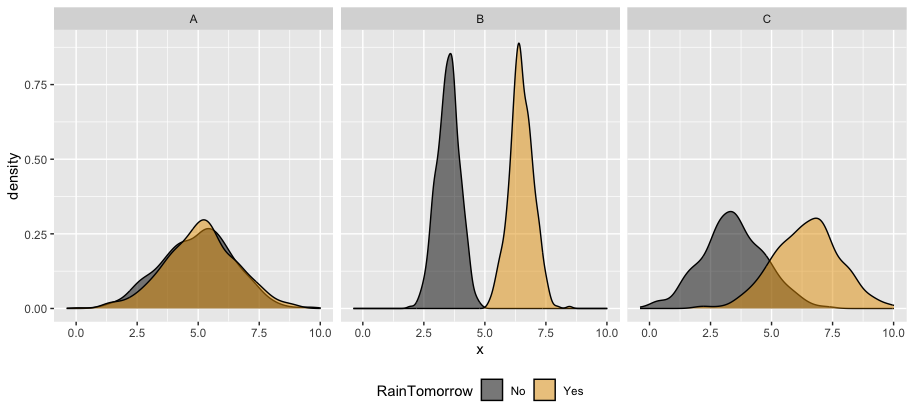
Which predictor is the “strongest” predictor of rain tomorrow?

. . .

The ROC curves corresponding to the models RainTomorrow ~ A, RainTomorrow ~ B, RainTomorrow ~ C are shown below.

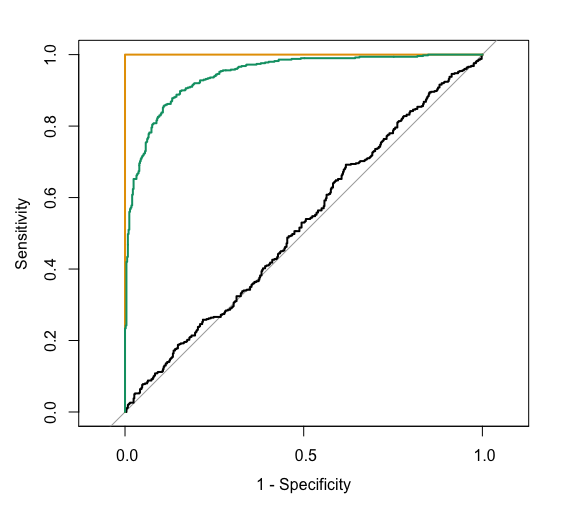
For each ROC curve, indicate the corresponding model and the approximate AUC. Do this in any order you want!

black ROC curve

  • RainTomorrow ~ ___
  • AUC is roughly ___

green ROC curve

  • RainTomorrow ~ ___
  • AUC is roughly ___.

orange ROC curve

  • RainTomorrow ~ ___
  • AUC is exactly ___.
Solution:

black ROC curve

  • RainTomorrow ~ A
  • AUC is roughly 0.5

green ROC curve

  • RainTomorrow ~ C
  • AUC is roughly .95.

orange ROC curve

  • RainTomorrow ~ B
  • AUC is exactly 1.

AUC Observation

In general:

  • A perfect classification model has an AUC of 1.
  • The simplest classification model that just randomly predicts y to be 1 or 0 (eg: by flipping a coin), has an AUC of 0.5. It is represented by the diagonal “no discrimination line” in an ROC plot.
  • A model with an AUC below 0.5 is worse than just random. Flipping a coin would be better.







Exercises

Today’s in-class exercises will be due as HW4.

Please find the exercises and template on Moodle.

I recommend working on Exercises 1, 5, and 6 in class.

Exercise 1 is necessary to the other exercises, and Exercises 5 and 6 involve new content: ROC curves, AUC, and LASSO for classification!







Wrapping Up

  • As usual, take time after class to finish any remaining exercises, check solutions, reflect on key concepts from today, and come to office hours with questions
  • Upcoming due dates:
    • TODAY: Quiz 1 Revisions
    • Thursday, October 31: HW4
  • Please install two packages before our next class: rpart and rpart.plot













Notes: R code

Let my_model be a logistic regression model of categorical response variable y using predictors x1 and x2 in our sample_data.