Motivating Question

GOAL

We have a quantitative response variable \(y\) and want to build a predictive regression model of \(y\) using a bunch of potential predictors \(x\).

BUT

The relationships between \(y\) and \(x\) are complicated, thus our existing modeling tools (e.g. least squares algorithm, LASSO) are too rigid. How can we build a flexible predictive regression model?

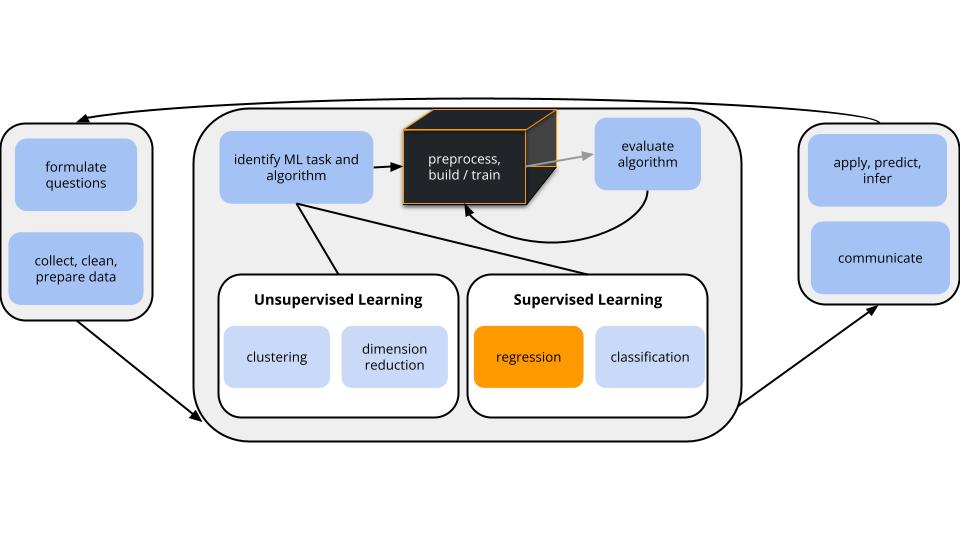
Parametric vs nonparametric models

The shared goal behind parametric and nonparametric regression models is to build a model of some quantitative response variable \(y\) using predictors \((x_1, x_2, ..., x_p)\):

\[y = f(x_1, x_2, ..., x_p) + \varepsilon\]

• parametric models
  Parametric regression models assume a specific “parametric” form for \(f\). For example, a linear regression model assumes that \(y\) is a linear combination of the predictors which is defined by parameters \(\beta_i\):
  \[y = f(x) + \varepsilon = \beta_0 + \beta_1x_1 + \cdots + \beta_p x_p + \varepsilon\]
  BUT this assumption can be too rigid and inflexible to describe the relationship between \(y\) and \(x\).

• nonparametric models
  Nonparametric models do NOT assume a parametric form for the relationship between \(y\) and \(x\), \(f(x_1, x_2, ..., x_p)\). Thus they are more flexible.

Common flexible regression models

1. K Nearest Neighbors (KNN)
2. Local regression / locally weighted scatterplot smoothing (LOESS) & generalized additive models (GAM)
3. Smoothing splines