15  Random forests & bagging

Settling In

  • Sit with the same group as last class.
    • Ask your groupmates what classes they are planning to take next semester!
  • Locate and open today’s QMD
  • Catch up on announcements and messages on Slack

Registration Tips

Thinking about what MSCS course to take next semester? Consider the following:

  • Interested in working with data (eg wrangling, plotting, data acquisition, advanced data processing)? Try:
    • COMP/STAT 112 (Intro to Data Science)
    • COMP/STAT 212 (Intermediate Data Science)
  • Interested in data and its connection to public health? Try:
    • STAT 125 (Epidemiology)
    • STAT 494 (Statistical Genetics)
  • Interested in developing a mathematical foundation for better/deeper understanding of statistical methodology? Try:
    • MATH/STAT 354 (Probability)
    • MATH/STAT 355 (Statistical Theory)
    • COMP/MATH 365 (Computational Linear Algebra)
  • Interested in learning some computing techniques that are fundamental to data science? Try:
    • COMP 123 (Core Concepts in Comp Sci)
    • COMP 127 (Object-Oriented Programming and Abstraction)
    • COMP 302 (Introduction to Database Management Systems)

NOTE: all of the highlighted courses above require permission of instructor to register. Fill out the corresponding interest form by the end of the day TODAY if you’re interested in taking any of these courses: https://www.macalester.edu/mscs/mscs-course-waitlists/


More generally, use this shiny app (created by Prof Brianna Heggeseth) to help explore courses being offered next semester: https://bheggeseth.shinyapps.io/Spring2025Courses/


Where Are We?

Let’s check out the table of contents in our textbook…

. . .

We’ve covered so far:

  • Chapter 2
  • Chapter 3
  • Chapter 4 (except 4.4–4.6, which we won’t cover)
  • Chapter 5
  • Chapter 6 (except 6.3, but we’ll get there)
  • Chapter 7 (we focused on 7.1, 7.6–7.7)
  • Chapter 8 (doing more today…)

. . .

After this, we’ll cover:

  • Chapter 12
  • Chapter 6.3

. . .

Curious about some of the other chapters?

  • Chapters 9 and 13: take Statistical Genetics
  • Chapter 10: take Introduction to Artificial Intelligence
  • Chapter 11: take Survival Analysis




Small Group Discussion

Discuss the following examples with your group.

Context

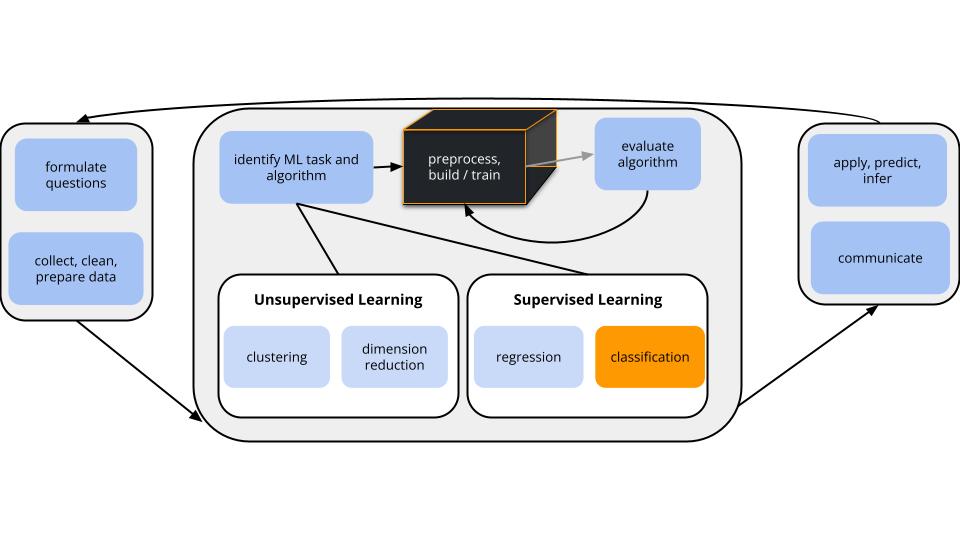
Within the broader machine learning landscape, we left off by discussing supervised classification techniques:

  • build a model of categorical variable y by predictors x
    • parametric model: logistic regression
    • nonparametric models: KNN & trees
  • evaluate the model
    We can use CV & in-sample techniques to estimate the accuracy of our classification models.
    • for binary y: sensitivity, specificity, ROC curves
    • for y with any number of categories: overall accuracy rates, category specific accuracy rates


TODAY’S GOAL

Add more nonparametric algorithms to our toolkit: random forests & bagging


EXAMPLE 1: Anticipation

What does the word “forest” mean to you?


EXAMPLE 2: Candy!!!

fivethirtyeight article

the experiment

library(tidyverse)
library(tidymodels)
library(rpart)        # for building trees
library(rpart.plot)   # for plotting trees
library(randomForest) # for bagging & forests
library(infer)        # for resampling

library(fivethirtyeight)
data("candy_rankings")
head(candy_rankings)
# A tibble: 6 × 13
  competitorname chocolate fruity caramel peanutyalmondy nougat crispedricewafer
  <chr>          <lgl>     <lgl>  <lgl>   <lgl>          <lgl>  <lgl>           
1 100 Grand      TRUE      FALSE  TRUE    FALSE          FALSE  TRUE            
2 3 Musketeers   TRUE      FALSE  FALSE   FALSE          TRUE   FALSE           
3 One dime       FALSE     FALSE  FALSE   FALSE          FALSE  FALSE           
4 One quarter    FALSE     FALSE  FALSE   FALSE          FALSE  FALSE           
5 Air Heads      FALSE     TRUE   FALSE   FALSE          FALSE  FALSE           
6 Almond Joy     TRUE      FALSE  FALSE   TRUE           FALSE  FALSE           
# ℹ 6 more variables: hard <lgl>, bar <lgl>, pluribus <lgl>,
#   sugarpercent <dbl>, pricepercent <dbl>, winpercent <dbl>


Write R code to find out the following:

# What are the 6 most popular candies?


# The least popular?
Solution: 
# What are the 6 most popular candies?
## OPTION 1
candy_rankings %>% 
  arrange(desc(winpercent)) %>% 
  head()
# A tibble: 6 × 13
  competitorname chocolate fruity caramel peanutyalmondy nougat crispedricewafer
  <chr>          <lgl>     <lgl>  <lgl>   <lgl>          <lgl>  <lgl>           
1 Reese's Peanu… TRUE      FALSE  FALSE   TRUE           FALSE  FALSE           
2 Reese's Minia… TRUE      FALSE  FALSE   TRUE           FALSE  FALSE           
3 Twix           TRUE      FALSE  TRUE    FALSE          FALSE  TRUE            
4 Kit Kat        TRUE      FALSE  FALSE   FALSE          FALSE  TRUE            
5 Snickers       TRUE      FALSE  TRUE    TRUE           TRUE   FALSE           
6 Reese's pieces TRUE      FALSE  FALSE   TRUE           FALSE  FALSE           
# ℹ 6 more variables: hard <lgl>, bar <lgl>, pluribus <lgl>,
#   sugarpercent <dbl>, pricepercent <dbl>, winpercent <dbl>
## OPTION 2
candy_rankings %>%
  slice_max(winpercent, n = 6)
# A tibble: 6 × 13
  competitorname chocolate fruity caramel peanutyalmondy nougat crispedricewafer
  <chr>          <lgl>     <lgl>  <lgl>   <lgl>          <lgl>  <lgl>           
1 Reese's Peanu… TRUE      FALSE  FALSE   TRUE           FALSE  FALSE           
2 Reese's Minia… TRUE      FALSE  FALSE   TRUE           FALSE  FALSE           
3 Twix           TRUE      FALSE  TRUE    FALSE          FALSE  TRUE            
4 Kit Kat        TRUE      FALSE  FALSE   FALSE          FALSE  TRUE            
5 Snickers       TRUE      FALSE  TRUE    TRUE           TRUE   FALSE           
6 Reese's pieces TRUE      FALSE  FALSE   TRUE           FALSE  FALSE           
# ℹ 6 more variables: hard <lgl>, bar <lgl>, pluribus <lgl>,
#   sugarpercent <dbl>, pricepercent <dbl>, winpercent <dbl>
# The least popular?
## OPTION 1
candy_rankings %>% 
  arrange(winpercent) %>% 
  head()
# A tibble: 6 × 13
  competitorname chocolate fruity caramel peanutyalmondy nougat crispedricewafer
  <chr>          <lgl>     <lgl>  <lgl>   <lgl>          <lgl>  <lgl>           
1 Nik L Nip      FALSE     TRUE   FALSE   FALSE          FALSE  FALSE           
2 Boston Baked … FALSE     FALSE  FALSE   TRUE           FALSE  FALSE           
3 Chiclets       FALSE     TRUE   FALSE   FALSE          FALSE  FALSE           
4 Super Bubble   FALSE     TRUE   FALSE   FALSE          FALSE  FALSE           
5 Jawbusters     FALSE     TRUE   FALSE   FALSE          FALSE  FALSE           
6 Root Beer Bar… FALSE     FALSE  FALSE   FALSE          FALSE  FALSE           
# ℹ 6 more variables: hard <lgl>, bar <lgl>, pluribus <lgl>,
#   sugarpercent <dbl>, pricepercent <dbl>, winpercent <dbl>
## OPTION 2
candy_rankings %>%
  slice_min(winpercent, n = 6)
# A tibble: 6 × 13
  competitorname chocolate fruity caramel peanutyalmondy nougat crispedricewafer
  <chr>          <lgl>     <lgl>  <lgl>   <lgl>          <lgl>  <lgl>           
1 Nik L Nip      FALSE     TRUE   FALSE   FALSE          FALSE  FALSE           
2 Boston Baked … FALSE     FALSE  FALSE   TRUE           FALSE  FALSE           
3 Chiclets       FALSE     TRUE   FALSE   FALSE          FALSE  FALSE           
4 Super Bubble   FALSE     TRUE   FALSE   FALSE          FALSE  FALSE           
5 Jawbusters     FALSE     TRUE   FALSE   FALSE          FALSE  FALSE           
6 Root Beer Bar… FALSE     FALSE  FALSE   FALSE          FALSE  FALSE           
# ℹ 6 more variables: hard <lgl>, bar <lgl>, pluribus <lgl>,
#   sugarpercent <dbl>, pricepercent <dbl>, winpercent <dbl>



EXAMPLE 3: Build an unpruned tree

For demonstration purposes only let’s:

  • define a popularity variable that categorizes the candies as “low”, “medium”, or “high” popularity
  • delete the original winpercent variable
  • rename variables to make them easier to read in a tree
  • make the candy name a row label, not a predictor
candy <- candy_rankings %>% 
  mutate(popularity = cut(winpercent, breaks = c(0, 40, 60, 100), labels = c("low", "med", "high"))) %>% 
  select(-winpercent) %>% 
  rename("price" = pricepercent, "sugar" = sugarpercent, "nutty" = peanutyalmondy, "wafer" = crispedricewafer) %>% 
  column_to_rownames("competitorname")

Our goal is to model candy popularity by all possible predictors in our data.

# STEP 1: tree specification
tree_spec <- decision_tree() %>%
  set_mode("classification") %>% 
  set_engine(engine = "rpart") %>% 
  set_args(cost_complexity = 0, min_n = 2, tree_depth = 30)

# STEP 2: Build the tree! No tuning (hence no workflows) necessary.
original_tree <- tree_spec %>% 
  fit(popularity ~ ., data = candy)

# Plot the tree
original_tree %>% 
  extract_fit_engine() %>% 
  plot(margin = 0) 
original_tree %>% 
  extract_fit_engine() %>% 
  text(cex = 0.7)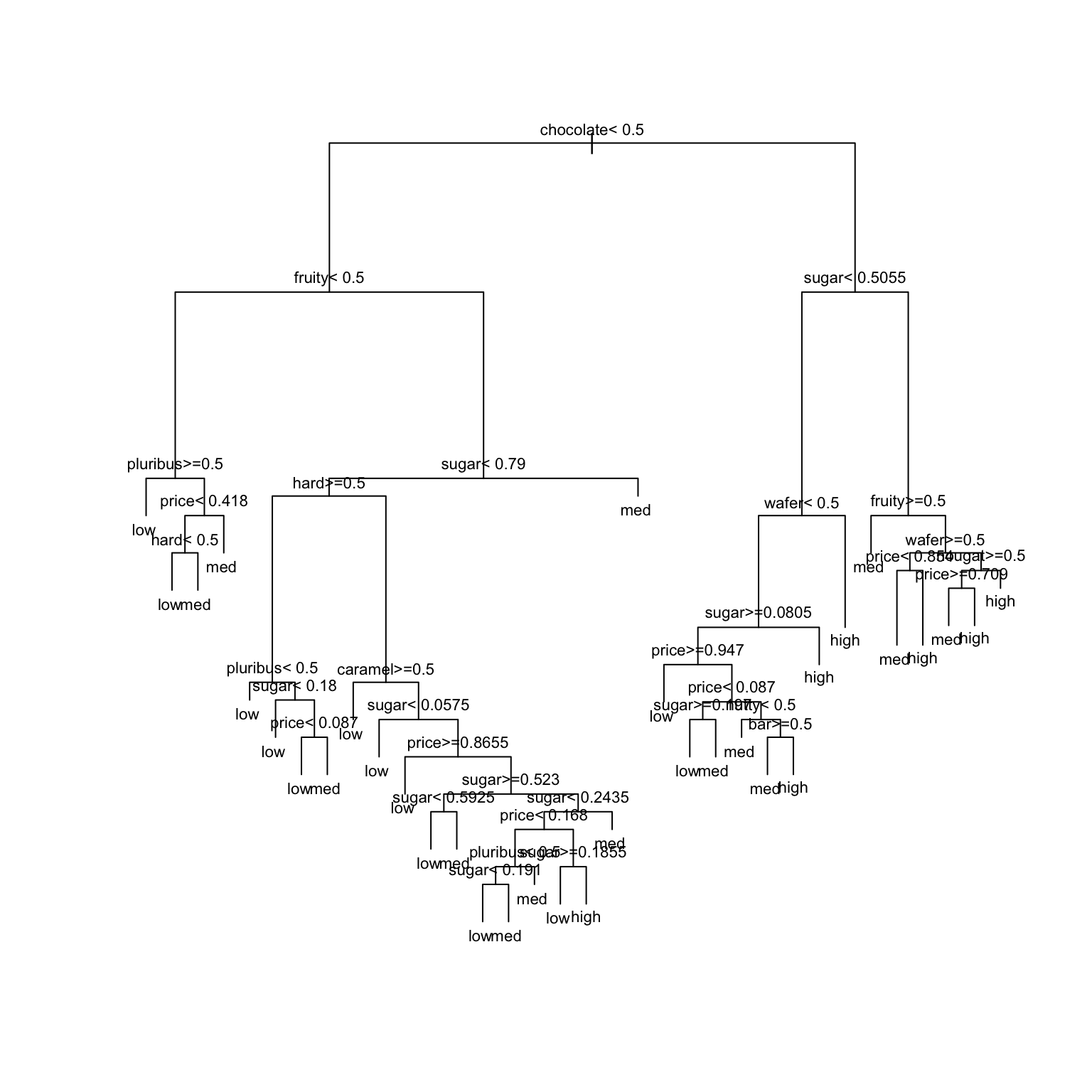

Ideally, our classification algorithm would have both low bias and low variance:

  • low variance = the results wouldn’t change much if we changed up the data set
  • low bias = within any data set, the predictions of y tend to have low error / high accuracy

Unfortunately, like other overfit algorithms, unpruned trees don’t enjoy both of these. They have…

  • low bias, low variance
  • low bias, high variance
  • high bias, low variance
  • high bias, high variance
Solution: low bias, high variance



New Concept

GOAL

Maintain the low bias of an unpruned tree while decreasing variance.


APPROACH

Build a bunch of unpruned trees from different data. This way, our final result isn’t overfit to our sample data.


THE RUB (CHALLENGE/DIFFICULTY)

We only have 1 set of data…


EXAMPLE 4: Take a REsample of candy

We only have 1 sample of data. But we can resample it (basically pretending we have a different sample).

Let’s each take our own unique candy resample (aka bootstrapping):

  • Take a sample of 85 candies from the original 85 candies, with replacement.
  • Some data points will be sampled multiple times while others aren’t sampled at all.
  • On average, 2/3 of the original data points will show up in the resample and 1/3 will be left out.

Take your resample:

# Set the seed to YOUR phone number (just the numbers)
set.seed(123456789)

# Take a REsample of candies from our sample
my_candy <- sample_n(candy, size = nrow(candy), replace = TRUE)

# Check it out
head(my_candy, 3)
                     chocolate fruity caramel nutty nougat wafer  hard   bar
Snickers Crisper...1      TRUE  FALSE    TRUE  TRUE  FALSE  TRUE FALSE  TRUE
Fruit Chews...2          FALSE   TRUE   FALSE FALSE  FALSE FALSE FALSE FALSE
Nestle Crunch...3         TRUE  FALSE   FALSE FALSE  FALSE  TRUE FALSE  TRUE
                     pluribus sugar price popularity
Snickers Crisper...1    FALSE 0.604 0.651        med
Fruit Chews...2          TRUE 0.127 0.034        med
Nestle Crunch...3       FALSE 0.313 0.767       high

In the next exercise, we’ll each build a tree of popularity using our own resample data.

First, check your intuition:

  1. TRUE / FALSE: All of our trees will be the same.
  2. TRUE / FALSE: Our trees will use the same predictor (but possibly a different cut-off) in the first split.
  3. TRUE / FALSE: Our trees will use the same predictors in all splits.
Solution:
  1. FALSE
  2. FALSE
  3. FALSE



Fun Math Facts:

With resampling (also known as bootstrapping), we have an original sample of \(n\) rows. We drawn individual rows with replacement from this set until we have another set of size \(n\).

The probability of choosing any one row (say the 1st row) on the first draw is \(1/n\). The probability of not choosing that one row is \(1-1/n\). That is just for the first draw. There are \(n\) draws, all of which are independent, so the probability of never choosing this particular row on any of the draws is \((1-1/n)^n\).

If we consider larger and larger datasets (large \(n\) going to infinity), then

\[\lim_{n \rightarrow \infty} (1-1/n)^n = 1/e \approx 0.368\]

Thus, the probability that any one row is NOT chosen is about 1/3 and the probability that any one row is chosen is 2/3.



EXAMPLE 5: Build & share YOUR tree

Build and plot a tree using your unique sample (my_candy):

Code 
# Build your tree
my_tree <- tree_spec %>% 
  fit(popularity ~ ., data = my_candy)

# Plot your tree
my_tree %>% 
  extract_fit_engine() %>% 
  plot(margin = 0) 
my_tree %>% 
  extract_fit_engine() %>% 
  text(cex = 0.7)

Use your tree to classify Baby Ruth, the 7th candy in the original data.

Code 
my_tree %>% 
  predict(new_data = candy[7,])

Finally, share your results!

Record your prediction and paste a picture of your tree into this document.


EXAMPLE 6: Using our FOREST

We now have a group of multiple trees – a forest!

These trees…

  • differ from resample to resample
  • don’t use the same predictor in each split (not even in the first split)!
  • produce different popularity predictions for Baby Ruth

  1. Based on our forest of trees (not just your 1 tree), what’s your prediction for Baby Ruth’s popularity?

  2. What do you think are the advantages of predicting candy popularity using a forest instead of a single tree?

  3. Can you anticipate any drawbacks of using forests instead of trees?

Solution:
  1. take the majority vote, i.e. most common category
  2. by averaging across multiple trees, classifications will be more stable / less variable from dataset to dataset (lower variance)
  3. computational intensity (lack of efficiency)



Notes: Bagging and Forests

BAGGING (Bootstrap AGGregatING) & Random Forests

To classify a categorical response variable y using a set of p predictors x:

  • Take B resamples from the original sample.

    • Sample WITH replacement
    • Sample size = original sample size n

  • Use each resample to build an unpruned tree.

    • For bagging: consider all p predictors in each split of each tree
    • For random forests: at each split in each tree, randomly select and consider only a subset of the predictors (often roughly p/2 or \(\sqrt{p}\))

  • Use each of the B trees to classify y at a set of predictor values x.

  • Average the classifications using a majority vote: classify y as the most common classification among the B trees.


Ensemble Methods

Bagging and random forest algorithms are ensemble methods.

They combine the outputs of multiple machine learning algorithms.

As a result, they decrease variability from sample to sample, hence provide more stable predictions / classifications than might be obtained by any algorithm alone.


EXAMPLE 7: pros & cons

  1. Order trees, forests, & bagging algorithms from least to most computationally expensive.
  2. What results will be easier to interpret: trees or forests?
  3. Which of bagging or forests will produce a collection of trees that tend to look very similar to each other, and similar to the original tree? Hence which of these algorithms is more dependent on the sample data, thus will vary more if we change up the data? [both questions have the same answer]
Solution:
  1. trees, forests, bagging
  2. trees (we can’t draw a forest)
  3. bagging (forests tend to have lower variability)



Exercises

For the rest of the class, work together on Exercises 1–7

  1. Tuning parameters (challenge)

Our random forest of popularity by all 11 possible predictors will depend upon 3 tuning parameters:

  • trees = the number of trees in the forest
  • mtry = number of predictors to randomly choose & consider at each split
  • min_n = minimum number of data points in any leaf node of any tree

Check your intuition.

  1. Does increasing the number of trees make the forest algorithm more or less variable from dataset to dataset?
  2. We have 11 possible predictors, and sqrt(11) is roughly 3. Recall: Would considering just 3 randomly chosen predictors in each split (instead of all 11) make the forest algorithm more or less variable from dataset to dataset?
  3. Recall that using unpruned trees in our forest is important to maintaining low bias. Thus should min_n be small or big?
Solution:
  1. less variable (less impacted by “unlucky” trees)
  2. less variable
  3. small



  1. Build the forest
    Given that forests are relatively computationally expensive, we’ll only build one forest using the following tuning parameters:
  • mtry = NULL: this sets mtry to the default, which is sqrt(number of predictors)
  • trees = 500
  • min_n = 2

Fill in the below code to run this forest algorithm.

# There's randomness behind the splits!
set.seed(253)
    
# STEP 1: Model Specification
rf_spec <- rand_forest()  %>%
  set_mode("___") %>%
  ___(engine = "ranger") %>% 
  ___(
    mtry = NULL,
    trees = 500,
    min_n = 2,
    probability = FALSE,    # Report classifications, not probability calculations
    importance = "impurity" # Use Gini index to measure variable importance
  )
    
# STEP 2: Build the forest
# There are no preprocessing steps or tuning, hence no need for a workflow!
candy_forest <- ___ %>% 
  fit(___, ___)
Solution: 
# There's randomness behind the splits!
set.seed(253)
    
# STEP 1: Model Specification
rf_spec <- rand_forest()  %>%
  set_mode("classification") %>%
  set_engine(engine = "ranger") %>% 
  set_args(
    mtry = NULL,
    trees = 500,
    min_n = 2,
    probability = FALSE, # give classifications, not probability calculations
    importance = "impurity" # use Gini index to measure variable importance
  )
    
# STEP 2: Build the forest
# There are no preprocessing steps or tuning, hence no need for a workflow!
candy_forest <- rf_spec %>% 
  fit(popularity ~ ., data = candy)



  1. Use the forest for prediction
    Use the forest to predict the popularity level for Baby Ruth. (Remember that its real popularity is “med”.)
candy_forest %>% 
  predict(new_data = candy[7,])
# A tibble: 1 × 1
  .pred_class
  <fct>      
1 med



  1. Evaluating forests: concepts

But how good is our forest at classifying candy popularity?

To this end, we could evaluate 3 types of forest predictions.

  1. Why don’t in-sample predictions, i.e. asking how well our forest classifies our sample candies, give us an “honest” assessment of our forest’s performance?
  2. Instead, suppose we used 10-fold cross-validation (CV) to estimate how well our forest classifies new candies. In this process, how many total trees would we need to construct?
  3. Alternatively, we can estimate how well our forest classifies new candies using the out-of-bag (OOB) error rate. Since we only use a resample of data points to build any given tree in the forest, the “out-of-bag” data points that do not appear in a tree’s resample are natural test cases for that tree. The OOB error rate tracks the proportion or percent of these out-of-bag test cases that are misclassified by their tree. How many total trees would we need to construct to calculate the OOB error rate?
  4. Moving forward, we’ll use OOB and not CV to evaluate forest performance. Why?
Solution:
  1. they use the same data we used to build the forest
  2. 10 forests * 500 trees each = 5000 trees
  3. 1 forest * 500 trees = 500 trees
  4. it’s much more computationally efficient



  1. Evaluating forests: implementation
  1. Report and interpret the estimated OOB prediction error.
candy_forest
parsnip model object

Ranger result

Call:
 ranger::ranger(x = maybe_data_frame(x), y = y, num.trees = ~500,      min.node.size = min_rows(~2, x), probability = ~FALSE, importance = ~"impurity",      num.threads = 1, verbose = FALSE, seed = sample.int(10^5,          1)) 

Type:                             Classification 
Number of trees:                  500 
Sample size:                      85 
Number of independent variables:  11 
Mtry:                             3 
Target node size:                 2 
Variable importance mode:         impurity 
Splitrule:                        gini 
OOB prediction error:             40.00 %
  1. The test or OOB confusion matrix provides more detail. Use this to confirm the OOB prediction error from part a. HINT: Remember to calculate error (1 - accuracy), not accuracy.
# NOTE: t() transposes the confusion matrix so that 
# the columns and rows are in the usual order
candy_forest %>% 
  extract_fit_engine() %>% 
  pluck("confusion.matrix") %>% 
  t()
         true
predicted low med high
     low    8   6    1
     med   15  29    6
     high   2   4   14

  1. Which level of candy popularity was least accurately classified by our forest?

  2. Check out the in-sample confusion matrix. In general, are the in-sample predictions better or worse than the OOB predictions?

# The cbind() includes the original candy data
# alongside their predicted popularity levels
candy_forest %>% 
  predict(new_data = candy) %>% 
  cbind(candy) %>% 
  conf_mat(
    truth = popularity,
    estimate = .pred_class
  )
          Truth
Prediction low med high
      low   18   0    0
      med    6  39    2
      high   1   0   19
Solution:
  1. We expect our forest to misclassify roughly 40% of new candies.
  2. .
# APPROACH 1: # of MISclassifications / total # of classifications
(6 + 1 + 15 + 6 + 2 + 4) / (8 + 29 + 14 + 6 + 1 + 15 + 6 + 2 + 4) 
[1] 0.4
# APPROACH 2: overall MISclassification rate = 1 - overall accuracy rate
# overall accuracy rate
(8 + 29 + 14) / (8 + 29 + 14 + 6 + 1 + 15 + 6 + 2 + 4) 
[1] 0.6
# overall misclassification rate
1 - 0.6
[1] 0.4
  1. low (more were classified as “med” than as “low”)
  2. much better!



  1. Variable importance

Variable importance metrics, averaged over all trees, measure the strength of the 11 predictors in classifying candy popularity:

# Print the metrics
candy_forest %>%
  extract_fit_engine() %>%
  pluck("variable.importance") %>% 
  sort(decreasing = TRUE)
    sugar     price chocolate    fruity     nutty     wafer  pluribus       bar 
9.4075750 9.0830343 5.0757837 2.8236876 2.2084982 2.1255274 1.8596475 1.8143452 
  caramel      hard    nougat 
1.6918086 1.3640697 0.9441936 
# Plot the metrics
library(vip)
candy_forest %>% 
  vip(geom = "point", num_features = 11)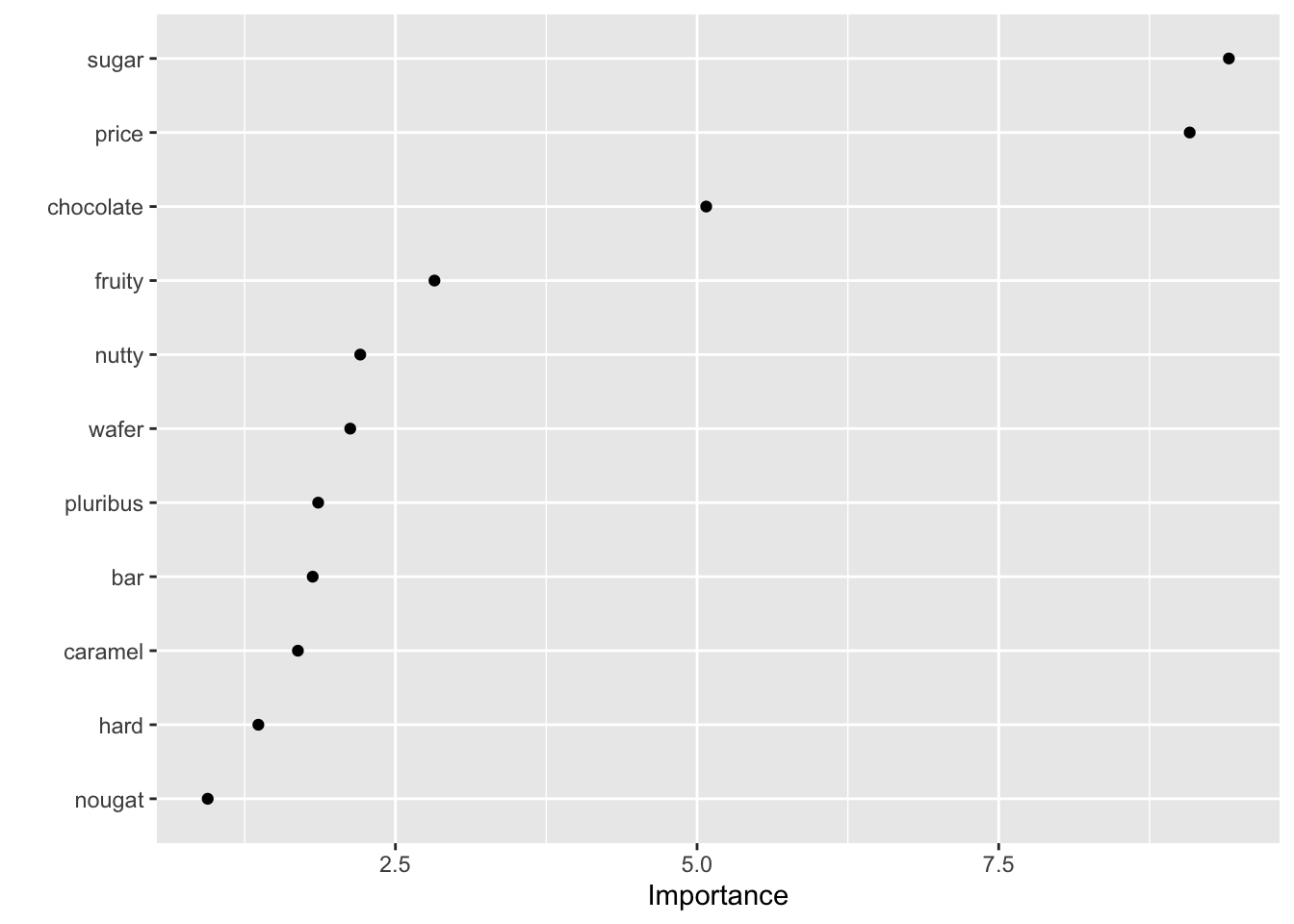

  1. If you’re a candy connoisseur, does this ranking make some contextual sense to you?
  2. The only 2 quantitative predictors, sugar and price, have the highest importance metrics. This could simply be due to their quantitative structure: trees tend to favor predictors with lots of unique values. Explain. HINT: A tree’s binary splits are identified by considering every possible cut / split point in every possible predictor.
Solution:
  1. will vary
  2. predictors with lots of unique values have far more possible split points to choose from




  1. Classification regions

Just like any classification model, forests divide our data points into classification regions.

Let’s explore this idea using some simulated data that illustrate some important contrasts.1

Import and plot the data:

# Import data
simulated_data <- read.csv("https://kegrinde.github.io/stat253_coursenotes/data/circle_sim.csv") %>% 
  mutate(class = as.factor(class))
    
# Plot data
ggplot(simulated_data, aes(y = X2, x = X1, color = class)) + 
  geom_point() + 
  theme_minimal()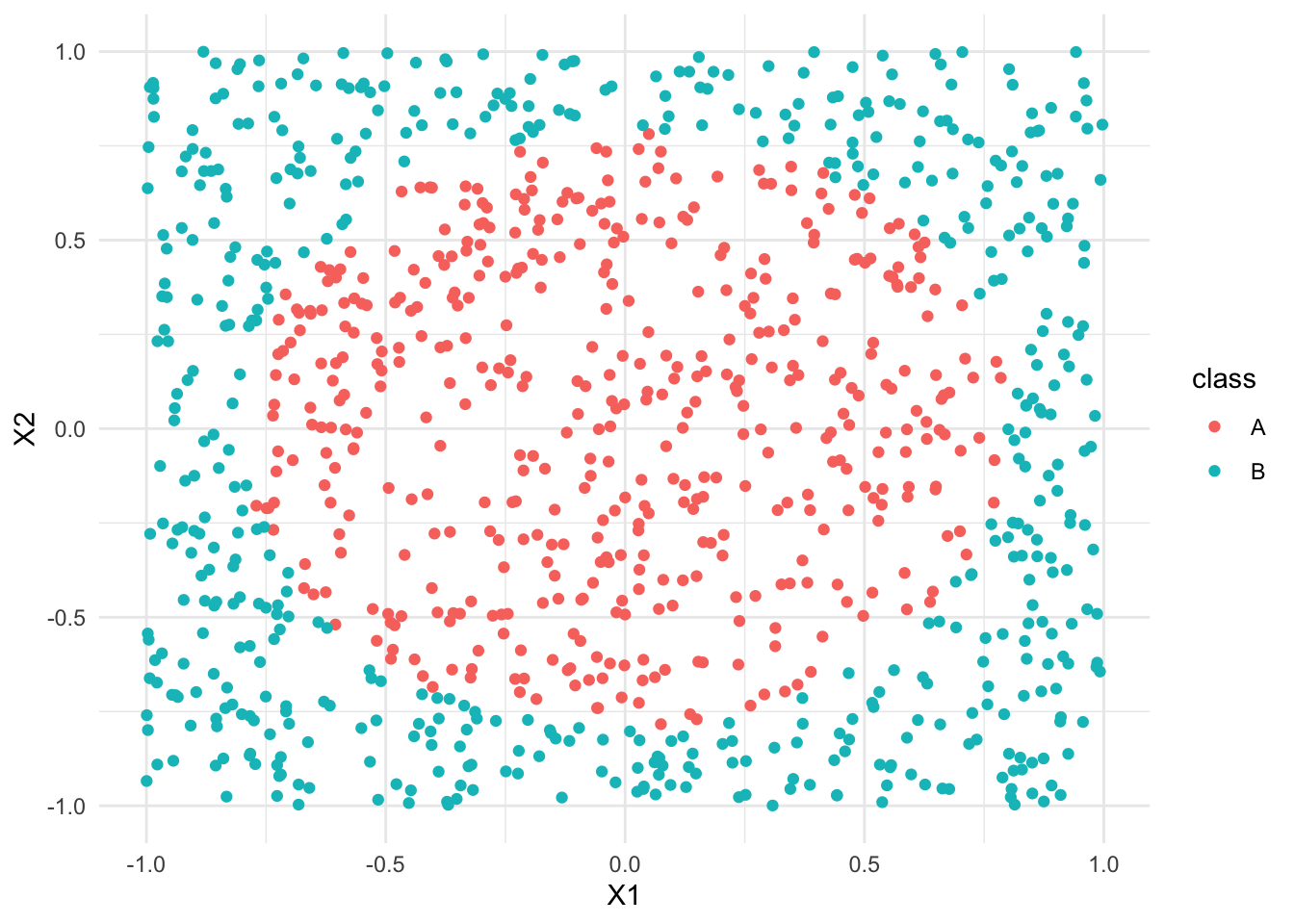

  1. Below is a classification tree of class by X1 and X2. What do you think its classification regions will look like?
# Build the (default) tree
circle_tree <- decision_tree() %>%
  set_mode("classification") %>% 
  set_engine(engine = "rpart") %>% 
  fit(class ~ ., data = simulated_data)

circle_tree %>% 
  extract_fit_engine() %>% 
  rpart.plot()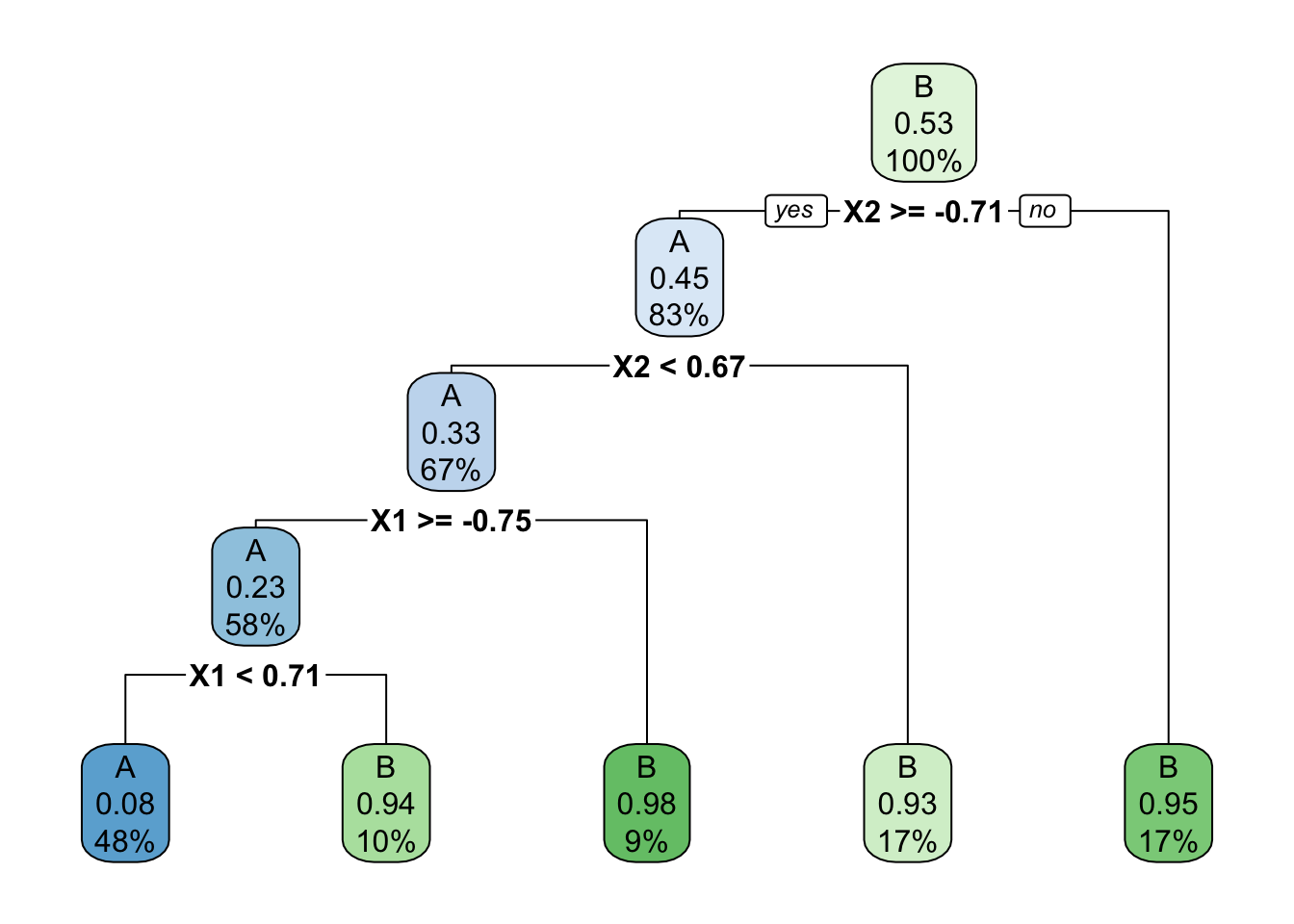

  1. Check your intuition. Were you right?
# THIS IS ONLY DEMO CODE.
# Plot the tree classification regions
examples <- data.frame(X1 = seq(-1, 1, len = 100), X2 = seq(-1, 1, len = 100)) %>% 
  expand.grid()

circle_tree %>% 
  predict(new_data = examples) %>% 
  cbind(examples) %>% 
  ggplot(aes(y = X2, x = X1, color = .pred_class)) + 
  geom_point() + 
  labs(title = "tree classification regions") + 
  theme_minimal()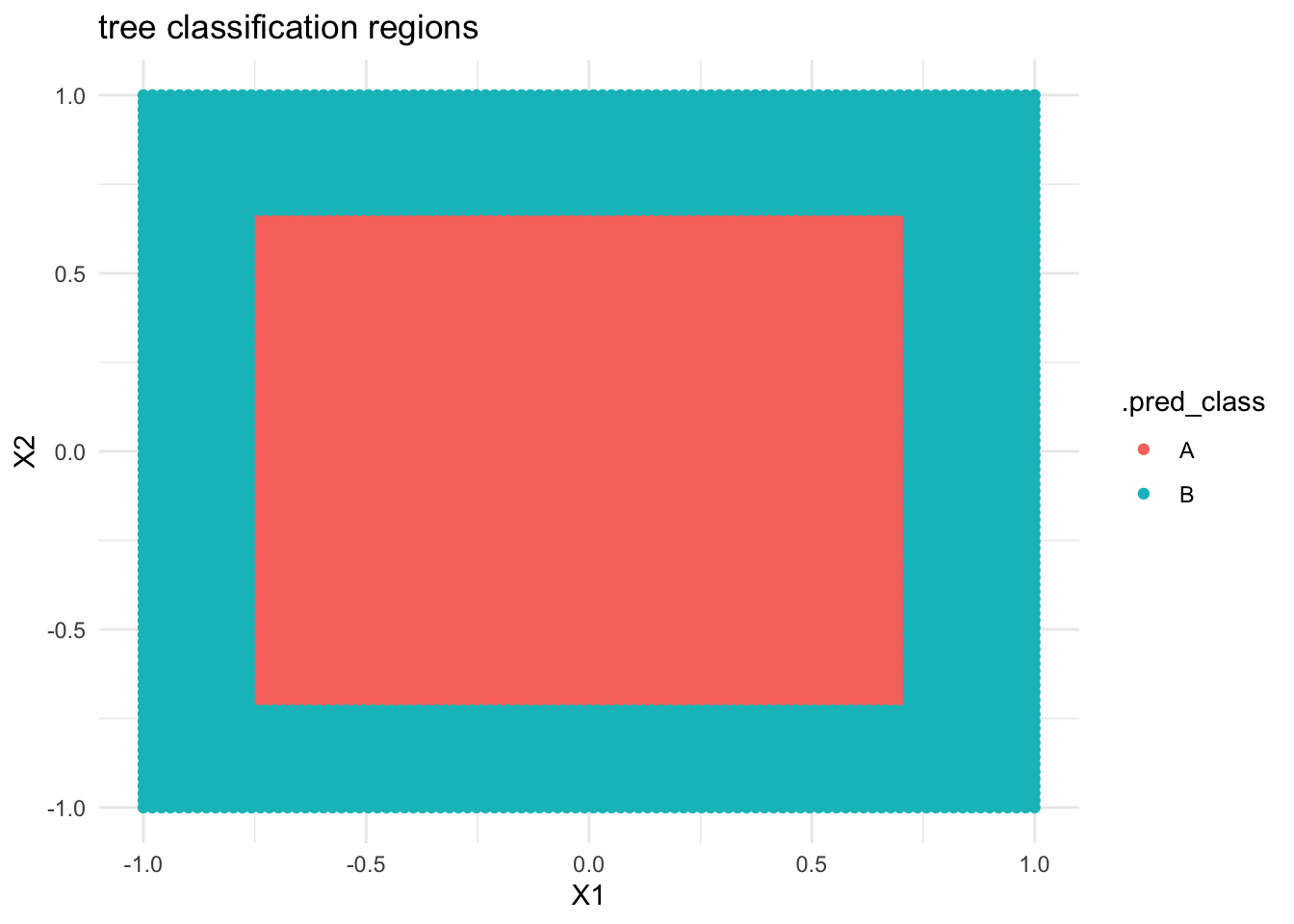

  1. If we built a forest model of class by X1 and X2, what do you think the classification regions will look like?

  2. Check your intuition. Were you right?

# THIS IS ONLY DEMO CODE.
# Build the forest
circle_forest <- rf_spec %>% 
  fit(class ~ ., data = simulated_data)

# Plot the tree classification regions
circle_forest %>% 
  predict(new_data = examples) %>% 
  cbind(examples) %>% 
  ggplot(aes(y = X2, x = X1, color = .pred_class)) + 
  geom_point() + 
  labs(title = "forest classification regions") + 
  theme_minimal()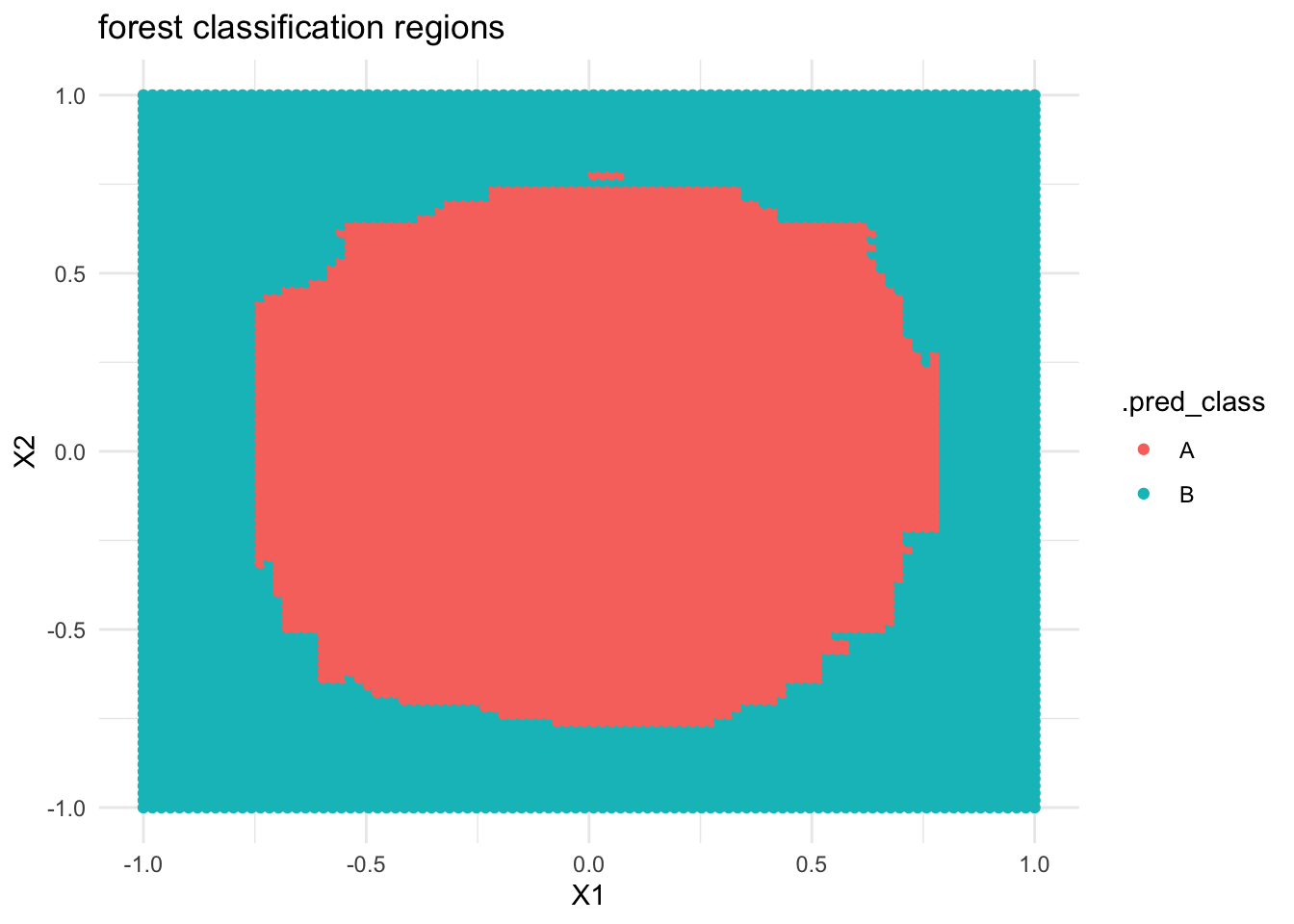

  1. Reflect on what you’ve observed here!
Solution:
  1. …
# THIS IS ONLY DEMO CODE.
# Plot the tree classification regions
examples <- data.frame(X1 = seq(-1, 1, len = 100), X2 = seq(-1, 1, len = 100)) %>% 
  expand.grid()

circle_tree %>% 
  predict(new_data = examples) %>% 
  cbind(examples) %>% 
  ggplot(aes(y = X2, x = X1, color = .pred_class)) + 
  geom_point() + 
  labs(title = "tree classification regions") + 
  theme_minimal()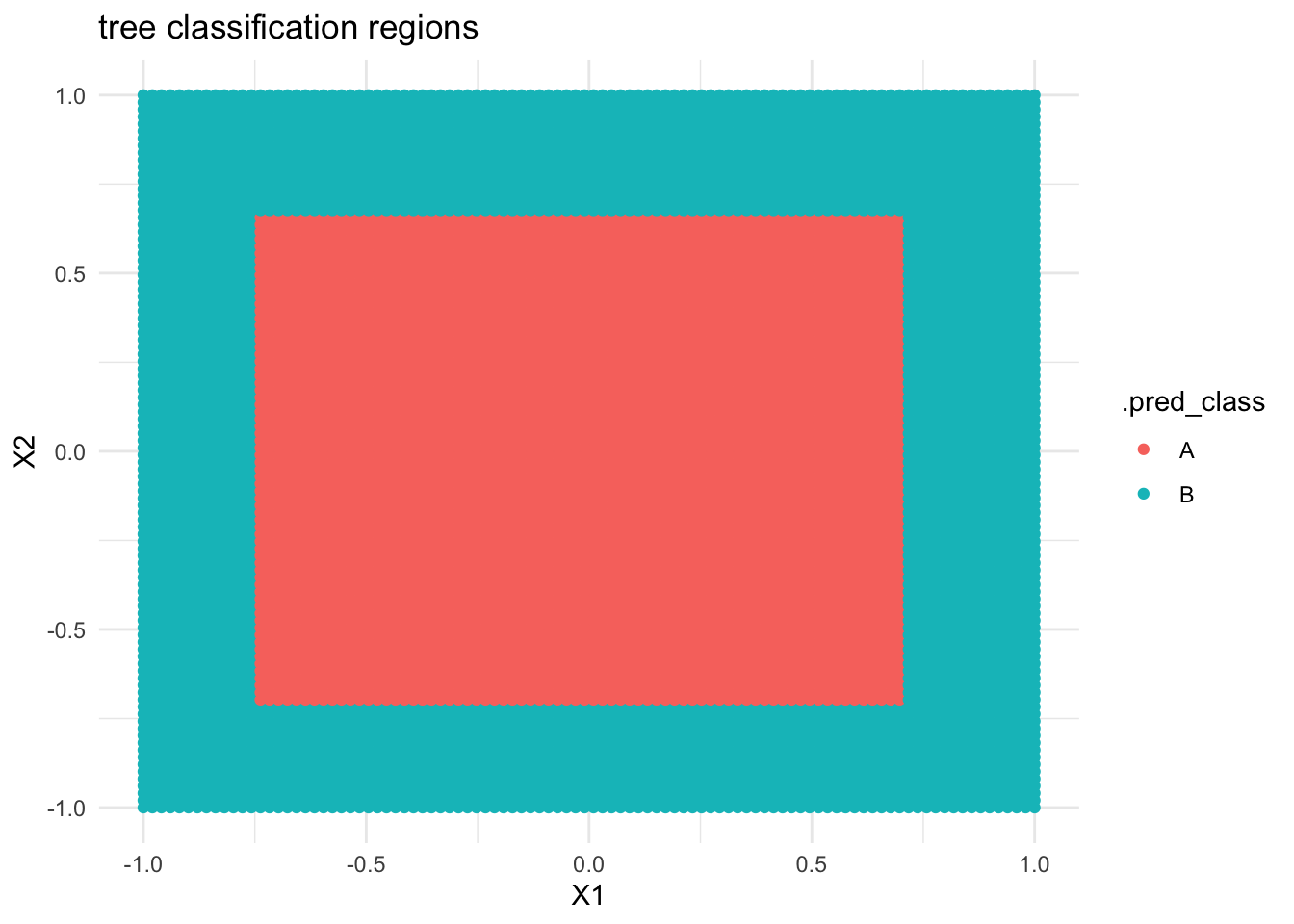

  1. …
# THIS IS ONLY DEMO CODE.
# Build the forest
circle_forest <- rf_spec %>% 
  fit(class ~ ., data = simulated_data)

# Plot the tree classification regions
circle_forest %>% 
  predict(new_data = examples) %>% 
  cbind(examples) %>% 
  ggplot(aes(y = X2, x = X1, color = .pred_class)) + 
  geom_point() + 
  labs(title = "forest classification regions") + 
  theme_minimal()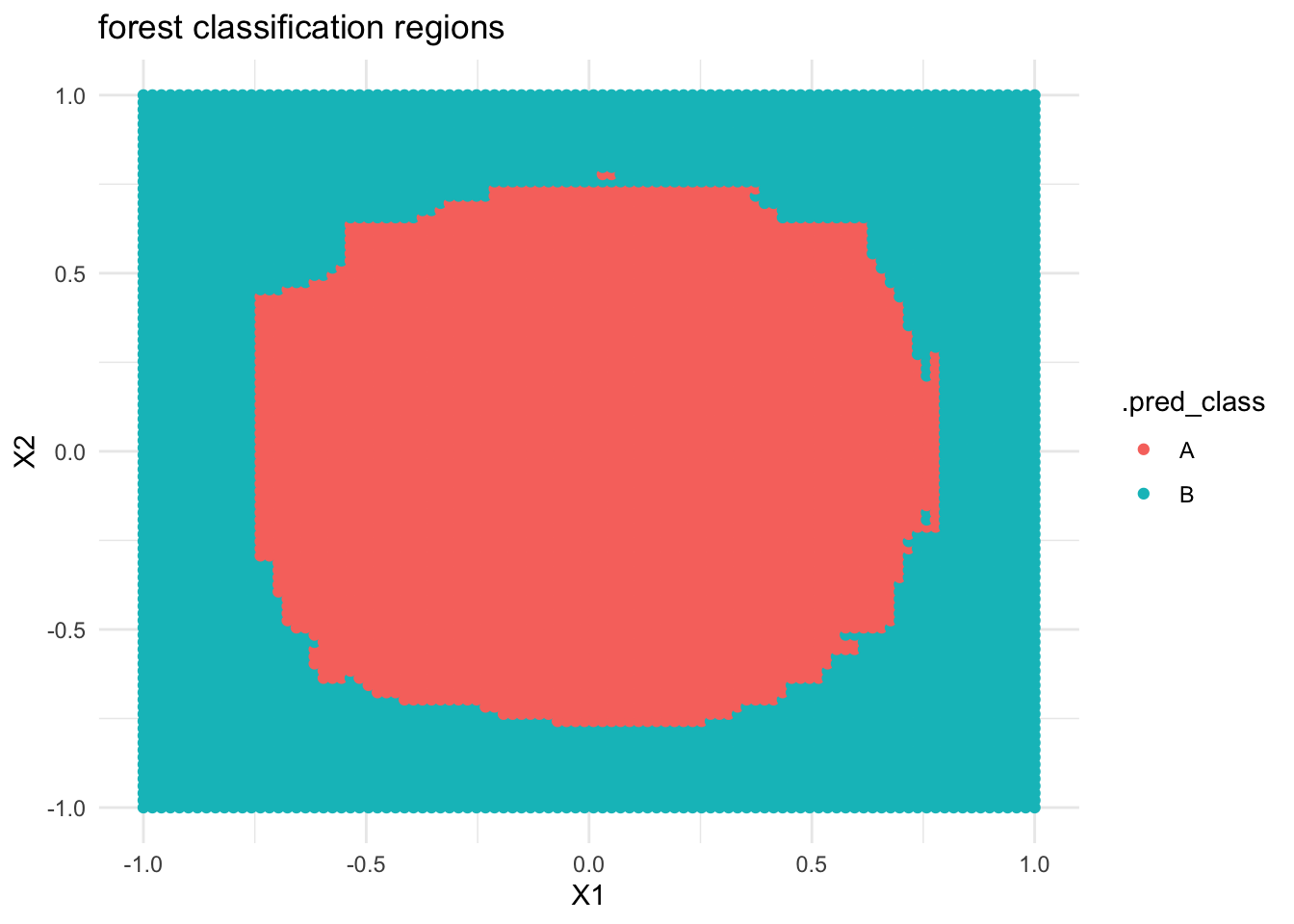

  1. Forest classification regions are less rigid / boxy than tree classification regions.



If you finish early

Do one of the following:

  • Check out the optional “Deeper learning” section below on another ensemble method: boosting.
  • Check out group assignment 2 on Moodle. Next class, your group will pick what topic to explore.
  • Work on homework.



Wrapping Up

  • As usual, take time after class to finish any remaining exercises, check solutions, reflect on key concepts from today, and come to office hours with questions
  • Upcoming due dates:
    • Before next class: CP11 (formal review of forests) AND review Group Assignment 2 instructions
    • Next Wednesday: HW5 and HW4 Revisions
    • Coming soon: Quiz 2 (Nov 19), Group Assignment 2 (Nov 26)



Deeper learning (optional)

Extreme gradient boosting, or XGBoost, is yet another ensemble algorithm for regression and classification. We’ll consider the big picture here. If you want to dig deeper:

  • Section 8.2.3 of the book provides a more detailed background
  • Julia Silge’s blogpost on predicting home runs provides an example of implementing XGBoost using tidymodels.

The big picture:

  • Like bagging and forests, boosting combines predictions from B different trees.

  • BUT these trees aren’t built from B different resamples. Boosting trees are grown sequentially, each tree slowly learning from the previous trees in the sequence to improve in areas where the previous trees didn’t do well. Loosely speaking, data points with larger misclassification rates among previous trees are given more weight in building future trees.

  • Unlike in bagging and forests, trees with better performance are given more weight in making future classifications.



Bagging vs boosting

  • Bagging typically helps decrease variance, but not bias. Thus it is useful in scenarios where other algorithms are unstable and overfit to the sample data.

  • Boosting typically helps decrease bias, but not variance. Thus it is useful in scenarios where other algorithms are stable, but overly simple.



Notes: R code

Suppose we want to build a forest or bagging algorithm of some categorical response variable y using predictors x1 and x2 in our sample_data.

# Load packages
library(tidymodels)
library(rpart)
library(rpart.plot)

# Resolves package conflicts by preferring tidymodels functions
tidymodels_prefer()



Make sure that y is a factor variable

sample_data <- sample_data %>% 
  mutate(y = as.factor(y))



Build the forest / bagging model

We’ll typically use the following tuning parameters:

  • trees = 500 (the more trees we use, the less variable the forest)
  • min_n = 2 (the smaller we allow the leaf nodes to be, the less pruned, hence less biased our forest will be)
  • mtry
    • for forests: mtry = NULL (the default) will use the “floor”, or biggest integer below, sqrt(number of predictors)
    • for bagging: set mtry to the number of predictors
# STEP 1: Model Specification
rf_spec <- rand_forest()  %>%
  set_mode("classification") %>%
  set_engine(engine = "ranger") %>% 
  set_args(
    mtry = ___,
    trees = 500,
    min_n = 2,
    probability = FALSE, # give classifications, not probability calculations
    importance = "impurity" # use Gini index to measure variable importance
  )

# STEP 2: Build the forest or bagging model
# There are no preprocessing steps or tuning, hence no need for a workflow!
ensemble_model <- rf_spec %>% 
  fit(y ~ x1 + x2, data = sample_data)



Use the model to make predictions / classifications

# Put in a data.frame object with x1 and x2 values (at minimum)
ensemble_model %>% 
  predict(new_data = ___)



Examine variable importance

# Print the metrics
ensemble_model %>%
  extract_fit_engine() %>%
  pluck("variable.importance") %>% 
  sort(decreasing = TRUE)

# Plot the metrics
# Plug in the number of top predictors you wish to plot
# (The upper limit varies by application!)
library(vip)
ensemble_model %>% 
  vip(geom = "point", num_features = ___)



Evaluate the classifications

# Out-of-bag (OOB) prediction error
ensemble_model

# OOB confusion matrix
ensemble_model %>% 
  extract_fit_engine() %>% 
  pluck("confusion.matrix") %>% 
  t()

# In-sample confusion matrix
ensemble_model %>% 
  predict(new_data = sample_data) %>% 
  cbind(sample_data) %>% 
  conf_mat(
    truth = y,
    estimate = .pred_class
  )

  1. citation: https://daviddalpiaz.github.io/r4sl/ensemble-methods.html#tree-versus-ensemble-boundaries↩︎