4  Cross-Validation

Settling In

  • Sit wherever you want, as long as there are 6 groups
    • Introduce yourselves / check in with each other

  • Catch up on any Slack messages you might have missed

  • You should have been notified of a “Stat 253 Feedback” Google Sheet shared with you – let me know if not! (example)

    • This is how you will access assignment feedback for this course. Take a minute to familiarize yourself with the document (and bookmark this link!).

  • Prepare to take notes.

Note-taking Tips

  • Go to the Schedule page
    • Locate and download the Quarto template (QMD) under the “In Class” materials for today.
  • Save this QMD in your “STAT 253 > Notes” folder
    • Render the QMD and check out the general structure
    • This is where you’ll work today! Use this however is best for your own learning — you won’t hand it in.
  • I encourage you to take hand-written notes (eg in a notebook) of key concepts and new code structures.



Learning Goals

  • Accurately describe all steps of cross-validation to estimate the test/out-of-sample version of a model evaluation metric
  • Explain what role CV has in a predictive modeling analysis and its connection to overfitting
  • Explain the pros/cons of higher vs. lower k in k-fold CV in terms of sample size and computing time
  • Implement cross-validation in R using the tidymodels package
  • Use these tools and concepts to inform and justify data analysis and modeling process



Notes: Cross-Validation

Context: Evaluating Regression Models

A reminder of our current context:

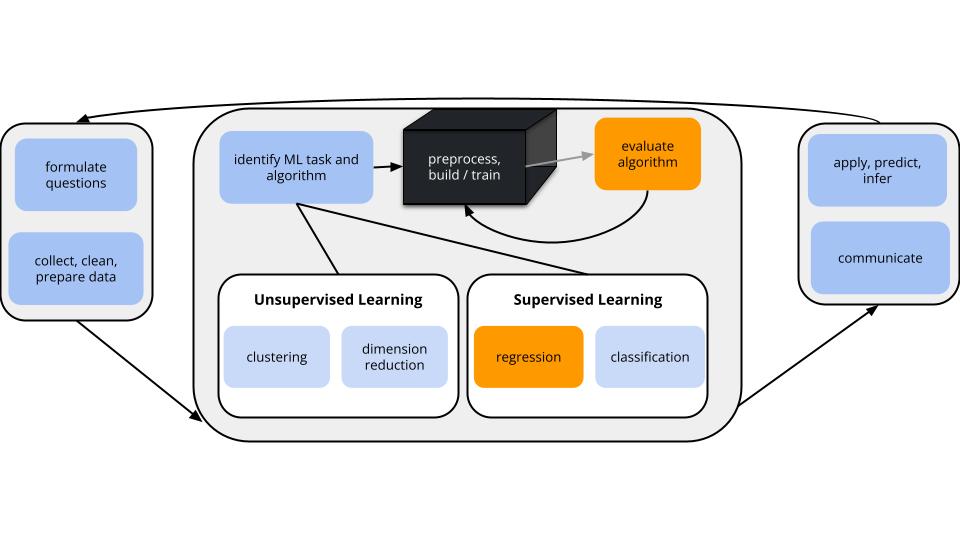
  • world = supervised learning
    We want to model some output variable \(y\) by some predictors \(x\).

  • task = regression
    \(y\) is quantitative

  • model = linear regression model via least squares algorithm
    We’ll assume that the relationship between \(y\) and \(x\) can be represented by

    \[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p + \varepsilon\]


GOAL: model evaluation

We want more honest metrics of prediction quality that

  1. assess how well our model predicts new outcomes; and
  2. help prevent overfitting.



Why is overfitting so bad?

Not only can overfitting produce misleading models, it can have serious societal impacts.

Examples:

  • Facial recognition algorithms are often overfit to the people who build them (who are not broadly representative of society). As one example, this has led to disproportionate bias in policing. For more on this topic, you might check out Coded Bias, a documentary by Shalini Kantayya which features MIT Media Lab researcher Joy Buolamwini.

  • Polygenic risk scores (PRSs), which aim to predict a person’s risk of developing a particular disease/trait based on their genetics, are often overfit to the data on which they are built (which, historically, has exclusively—or at least primarily—included individuals of European ancestry). As a result, PRS predictions tend to be more accurate in European populations and new research suggests that their continued use in clinical settings could exacerbate health disparities.

  • There are connections to overfitting in the article for the ethics reflection on HW1 (about a former Amazon recruiting algorithm).


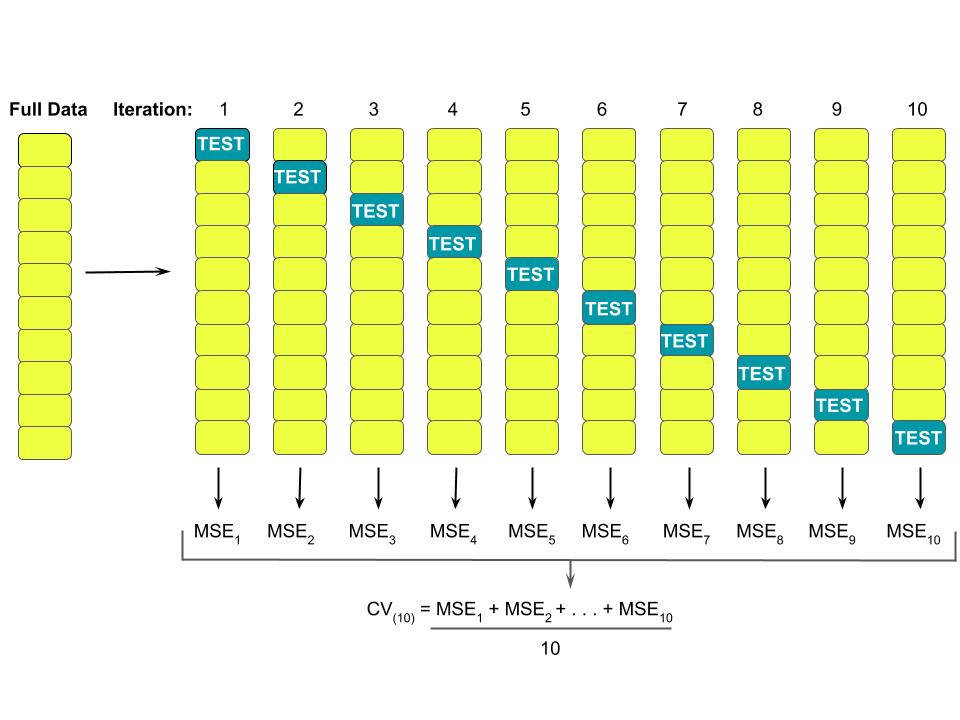
k-Fold Cross Validation

We can use k-fold cross-validation to estimate the typical error in our model predictions for new data:

  • Divide the data into \(k\) folds (or groups) of approximately equal size.
  • Repeat the following procedures for each fold \(j = 1,2,...,k\):
    • Remove fold \(j\) from the data set.
    • Fit a model using the data in the other \(k-1\) folds (training).
    • Use this model to predict the responses for the \(n_j\) cases in fold \(j\): \(\hat{y}_1, ..., \hat{y}_{n_j}\).
    • Calculate the MAE for fold \(j\) (testing): \(\text{MAE}_j = \frac{1}{n_j}\sum_{i=1}^{n_j} |y_i - \hat{y}_i|\).
  • Combine this information into one measure of model quality: \[\text{CV}_{(k)} = \frac{1}{k} \sum_{j=1}^k \text{MAE}_j\]



Small Group Discussion

Algorithms and Tuning

Definitions

  • algorithm = a step-by-step procedure for solving a problem (Merriam-Webster)

  • tuning parameter = a parameter or quantity upon which an algorithm depends, that must be selected or tuned to “optimize” the algorithm

1


Prompts

  1. Acting out 3-fold cross-validation
  • Modeling context:
    • We are evaluating a predictive model for height (in inches).
    • We’re going to use a simple intercept-only model, \[E[height] = \beta_0,\] to make this easier to do by hand.
    • You are the data. If you don’t know your height in inches, do that conversion now!
    • (The instructor will give out results for model fitting when you get to the relevant part in acting out the 3-fold CV process.)
  • Let’s act out 3-fold CV!
    • Step 1: …
    • Step 2: …
    • Etc.
  • Try again, with different folds.


  1. Conceptual check

  1. Why is \(k\)-fold cross-validation an algorithm?

  2. What is the tuning parameter of this algorithm and what values can this take?

  3. How is 2-fold cross-validation (CV) different from validation? (Validation is what we did last class: splitting our sample into a training dataset and a testing dataset.)

  4. Why might 3-fold CV be better than 2-fold CV?

  5. Why might LOOCV (leave-one-out CV) (k-fold CV where k = sample size) be worse than 3-fold cross-validation?

  6. Make a guess: what value of k do you think practitioners typically use?


  1. R Code Preview

We’ve been doing a 2-step process to build linear regression models using the tidymodels package:

# STEP 1: model specification
lm_spec <- linear_reg() %>%
  set_mode("regression") %>% 
  set_engine("lm")
  
# STEP 2: model estimation
my_model <- lm_spec %>% 
  fit(
    y ~ x1 + x2,
    data = sample_data
  )

For k-fold cross-validation, we can tweak STEP 2. Discuss the code below:

  • What’s similar? What’s different?
  • What do you think each new, or otherwise modified, line does?
  • Why do we need set.seed?
# k-fold cross-validation
set.seed(___)
my_model_cv <- lm_spec %>% 
  fit_resamples(
    y ~ x1 + x2, 
    resamples = vfold_cv(sample_data, v = ___), 
    metrics = metric_set(mae, rsq)
  )



Notes: R Code

NoteReminder

This section is for future reference. It is a summary of code you’ll learn below for doing k-fold cross-validation. You do not need to (and in fact should not) run the code in this section verbatim in R; it is example code and meant for future reference only.

Suppose we wish to build and evaluate a linear regression model of y vs x1 and x2 using our sample_data.

Load the appropriate packages

# Load packages
library(tidyverse)
library(tidymodels)

Obtain k-fold cross-validated estimates of MAE and \(R^2\)

(Review above for discussion of these steps.)

# model specification
lm_spec <- linear_reg() %>%
  set_mode("regression") %>% 
  set_engine("lm")

# k-fold cross-validation
# For "v", put your number of folds k
set.seed(___)
model_cv <- lm_spec %>% 
  fit_resamples(
    y ~ x1 + x2,
    resamples = vfold_cv(sample_data, v = ___), 
    metrics = metric_set(mae, rsq)
)

Obtain the cross-validated metrics

model_cv %>% 
  collect_metrics()

Get the MAE and R-squared for each test fold

# MAE for each test fold: Model 1
model_cv %>% 
  unnest(.metrics)



Exercises

Instructions

  • Go to the Course Schedule and find the QMD template for today
    • Save this in your STAT 253 Notes folder, NOT your downloads!
  • Work through the exercises implementing CV to compare two possible models predicting height
  • Same directions as before:
    • Be kind to yourself/each other
    • Collaborate
    • DON’T edit starter code (i.e., code with blanks ___). Instead, copy-paste into a new code chunk below and edit from there.
  • Ask me questions as I move around the room


Questions

# Load packages and data
library(tidyverse)
library(tidymodels)
humans <- read.csv("https://Mac-Stat.github.io/data/bodyfat50.csv") %>% 
  filter(ankle < 30) %>% 
  rename(body_fat = fatSiri)


  1. Review: In-sample metrics

Use the humans data to build two separate models of height:

# STEP 1: model specification
lm_spec <- ___() %>% 
  set_mode(___) %>% 
  set_engine(___)
# STEP 2: model estimation
model_1 <- ___ %>% 
  ___(height ~ hip + weight + thigh + knee + ankle, data = humans)
model_2 <- ___ %>% 
  ___(height ~ chest * age * weight * body_fat + abdomen + hip + thigh + knee + ankle + biceps + forearm + wrist, data = humans)

Calculate the in-sample R-squared for both models:

# IN-SAMPLE R^2 for model_1 = ???
model_1 %>% 
  ___()
# IN-SAMPLE R^2 for model_2 = ???
model_2 %>% 
  ___()

Calculate the in-sample MAE for both models:

# IN-SAMPLE MAE for model_1 = ???
model_1 %>% 
  ___(new_data = ___) %>% 
  mae(truth = ___, estimate = ___)
# IN-SAMPLE MAE for model_2 = ???
model_2 %>% 
  ___(new_data = ___) %>% 
  mae(truth = ___, estimate = ___)


  1. In-sample model comparison

Which model seems “better” by the in-sample metrics you calculated above? Any concerns about either of these models?


  1. 10-fold CV

Complete the code to run 10-fold cross-validation for our two models.

Model 1: height ~ hip + weight + thigh + knee + ankle
Model 2: height ~ chest * age * weight * body_fat + abdomen + hip + thigh + knee + ankle + biceps + forearm + wrist

# 10-fold cross-validation for model_1
set.seed(253)
model_1_cv <- ___ %>% 
  ___(
    ___,
    ___ = vfold_cv(___, v = ___), 
    ___ = metric_set(mae, rsq)
  )
# 10-fold cross-validation for model_2
set.seed(253)
model_2_cv <- ___ %>% 
  ___(
    ___,
    ___ = vfold_cv(___, v = ___), 
    ___ = metric_set(mae, rsq)
  )


  1. Calculating the CV MAE
  1. Use collect_metrics() to obtain the cross-validated MAE and \(R^2\) for both models.
# HINT
___ %>% 
  collect_metrics()
  1. Interpret the cross-validated MAE and \(R^2\) for model_1.


  1. Details: fold-by-fold results

The collect_metrics() function gave the final CV MAE, or the average MAE across all 10 test folds. If you want the MAE from each test fold, try unnest(.metrics).

  1. Obtain the fold-by-fold results for the model_1 cross-validation procedure using unnest(.metrics).
# HINT
___ %>% 
  unnest(.metrics)

  1. Which fold had the worst average prediction error and what was it?

  2. Recall that collect_metrics() reported a final CV MAE of 1.87 for model_1. Confirm this calculation by wrangling the fold-by-fold results from part a.


  1. Comparing models

The table below summarizes the in-sample and 10-fold CV MAE for both models.

Model IN-SAMPLE MAE 10-fold CV MAE
model_1 1.55 1.87
model_2 0.64 2.47

  1. Based on the in-sample MAE alone, which model appears better?

  2. Based on the CV MAE alone, which model appears better?

  3. Based on all of these results, which model would you pick?

  4. Do the in-sample and CV MAE suggest that model_1 is overfit to our humans sample data? What about model_2? Why/why not?


  1. LOOCV

No code to implement for this exercise–just answer the following conceptually.

  1. How could we adapt the code in Exercise 3 to use LOOCV MAE instead of the 10-fold CV MAE?

  2. Why do we technically not need to set.seed() for the LOOCV algorithm?


  1. Data drill
  1. Calculate the average height of people under 40 years old vs people 40+ years old.
  1. Plot height vs age among our subjects that are 30+ years old.
  1. Fix this code:
model_3<-lm_spec%>%fit(height~age,data=humans)
model_3%>%tidy()


  1. Reflection: Part 1

The “regular” exercises are over, but class is not done! Your group should agree to either work on HW1 or the remaining reflection questions.

This is the end of Unit 1 on “Regression: Model Evaluation”! Let’s reflect on the technical content of this unit:

  • What was the main motivation / goal behind this unit?
  • What are the four main questions that were important to this unit?
  • For each of the following tools, describe how they work and what questions they help us address:
    • R-squared
    • residual plots
    • out-of-sample MAE
    • in-sample MAE
    • validation
    • cross-validation
  • In your own words, define the following:
    • overfitting
    • algorithm
    • tuning parameter
  • Review the new tidymodels syntax from this unit. Identify key themes and patterns.

Just for fun–icons! You may have noticed that the left sidebar of our course website has icons for the top few pages. It would be nice to have icons for our main content activities too!

  • Go to https://icons.getbootstrap.com/ to browse the icons that are available.
  • Find an icon that is emblematic of the main content/ideas for each of our first 4 topics (Introductions & Overview, Model Evaluation, Overfitting, Cross-Validation).



Solutions

Small Group Discussion

  1. Conceptual Check
Solution

  1. It follows a list of steps to get to its goal.

  2. \(k\), the number of folds, is a tuning parameter. \(k\) can be any integer from 2, …, \(n\) where \(n\) is our sample size.

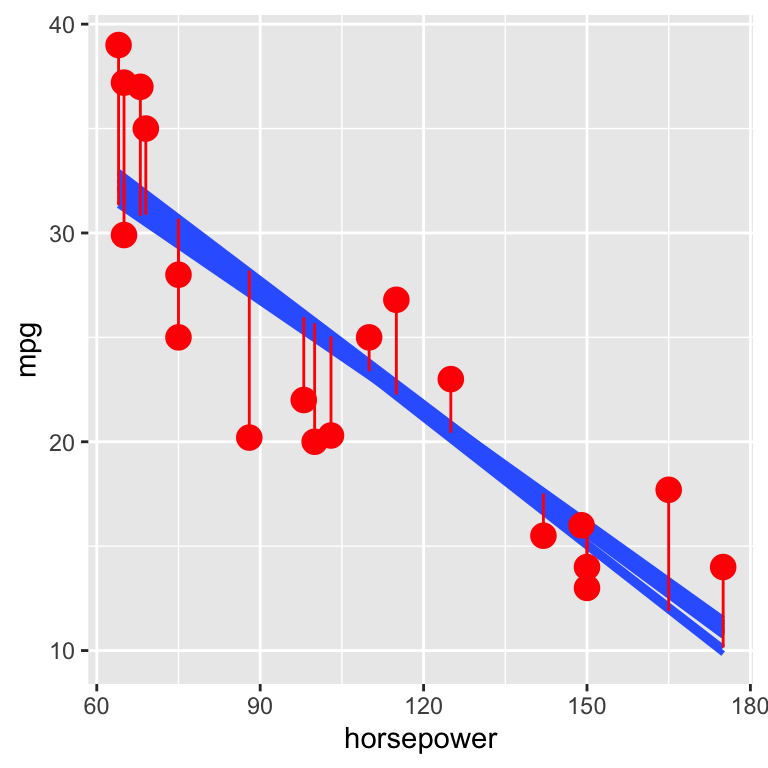
SPECIAL CASE: Leave One Out Cross-Validation (LOOCV).

LOOCV is a special case of k-fold cross-validation in which, in each iteration, we hold out one data point as a test case and use the other \(n-1\) data points for training. Thus LOOCV is equivalent to \(k = n\) fold CV.

In pictures: In the end, we fit \(n\) training models (blue lines) and test each on one test car (red dots).

  1. We use both groups as training and testing, in turn.

  2. We have a larger dataset to train our model on. We are less likely to get an unrepresentative set as our training data. We are also averaging our overall cross-validated MAE estimate over more testing folds, which is likely to result in a more stable estimate of out-of-sample error.

  3. Prediction error for 1 person is highly variable. Also, for computational time reasons, fitting \(n\) models can be very slow.

  4. In practice, \(k = 10\) and \(k=7\) are common choices for cross-validation. This has been shown to hit the ‘sweet spot’ between the extremes of \(k=n\) (LOOCV) and \(k=2\).

  • \(k=2\) only utilizes 50% of the data for each training model, thus might result in overestimating the prediction error
  • \(k=n\) leave-one-out cross-validation (LOOCV) requires us to build \(n\) training models, thus might be computationally expensive for larger sample sizes \(n\). Further, with only one data point in each test set, the training sets have a lot of overlap. This correlation among the training sets can make the ultimate corresponding estimate of prediction error less reliable.


  1. R Code Preview
Solution

What’s similar? What’s different? Similar to fit(), we tell the function fit_resamples what model to fit and which data to use. But, instead of fitting that model once to the full data, we use CV.

What does each line do?

set.seed(___) # set seed for reproducibility

my_model_cv <- lm_spec %>% # take the model specs we defined earlier, and then
  
  fit_resamples( # fit multiple models (across multiple resamples of the data)
    
    y ~ x1 + x2, # the model we want to fit
    
    resamples = vfold_cv(sample_data, v = ___), # use "v"-fold CV to create the resamples (fill in the blank to specify "v", aka "k")
    
    metrics = metric_set(mae, rsq) # specify which evaluation metric(s) (MAE, R^2) to use 
    
  )

Here are a few general tips for breaking down complex code:

  • Read the R Documentation / help page for any new functions (eg type ?fit_resamples into the Console)
  • Try removing or otherwise modifying each line of code and see what happens!
Why set a seed? The process of creating the folds is random, so we should set the seed to have reproducibility within our work.



Exercises

  1. Review: In-sample metrics
Solution 
# STEP 1: model specification
lm_spec <- linear_reg() %>% 
  set_mode("regression") %>% 
  set_engine("lm")

# STEP 2: model estimation
model_1 <- lm_spec %>% 
  fit(height ~ hip + weight + thigh + knee + ankle, data = humans)
model_2 <- lm_spec %>% 
  fit(height ~ chest * age * weight * body_fat + abdomen + hip + thigh + knee + ankle + biceps + forearm + wrist, data = humans)

# IN-SAMPLE R^2 for model_1 = 0.40
model_1 %>% 
  glance()
# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>   <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.401         0.310  1.98      4.42 0.00345     5  -78.8  172.  183.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>
# IN-SAMPLE R^2 for model_2 = 0.87
model_2 %>% 
  glance()
# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>   <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.874         0.680  1.35      4.51 0.00205    23  -48.4  147.  188.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>
# IN-SAMPLE MAE for model_1 = 1.55
model_1 %>% 
  augment(new_data = humans) %>% 
  mae(truth = height, estimate = .pred)
# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard        1.55
# IN-SAMPLE MAE for model_2 = 0.64
model_2 %>% 
  augment(new_data = humans) %>% 
  mae(truth = height, estimate = .pred)
# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard       0.646


  1. In-sample model comparison
Solution The in-sample metrics are better for model_2, but from experience in our previous class, we should expect this to be overfit.


  1. 10-fold CV
Solution 
# 10-fold cross-validation for model_1
set.seed(253)
model_1_cv <- lm_spec %>% 
  fit_resamples(
    height ~ hip + weight + thigh + knee + ankle,
    resamples = vfold_cv(humans, v = 10), 
    metrics = metric_set(mae, rsq)
  )

# STEP 2: 10-fold cross-validation for model_2
set.seed(253)
model_2_cv <- lm_spec %>% 
  fit_resamples(
    height ~ chest * age * weight * body_fat + abdomen + hip + thigh + knee + ankle + biceps + forearm + wrist,
    resamples = vfold_cv(humans, v = 10), 
    metrics = metric_set(mae, rsq)
  )


  1. Calculating the CV MAE
Solution 
# model_1
# CV MAE = 1.87, CV R-squared = 0.41
model_1_cv %>% 
  collect_metrics()
# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 mae     standard   1.87     10   0.159 Preprocessor1_Model1
2 rsq     standard   0.409    10   0.124 Preprocessor1_Model1
# model_2
# CV MAE = 2.47, CV R-squared = 0.53
model_2_cv %>% 
  collect_metrics()
# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 mae     standard   2.47     10   0.396 Preprocessor1_Model1
2 rsq     standard   0.526    10   0.122 Preprocessor1_Model1
  1. We expect our first model to explain roughly 40% of variability in height among new adults, and to produce predictions of height (for new adults) that are off by 1.9 inches on average.
Important

The in-sample MAE and CV MAE are not the same (conceptually or numerically), so our interpretation should be different, too!

To distinguish between the two, I like to add a phrase along the line of “for new adults” to my CV metric interpretations. Notice how I did this above for both the CV \(R^2\) and CV MAE. This “for new adults” phrase is one way of saying that these metrics are quantifying the model’s performance on new/test data — not the data it was trained on. This will be important to clarify any time we are interpreting a CV (or otherwise “out-of-sample”) metric!


  1. Details: fold-by-fold results
Solution 
# a. model_1 MAE for each test fold
model_1_cv %>% 
  unnest(.metrics) %>% 
  filter(.metric == "mae")
# A tibble: 10 × 7
   splits         id     .metric .estimator .estimate .config           .notes  
   <list>         <chr>  <chr>   <chr>          <dbl> <chr>             <list>  
 1 <split [35/4]> Fold01 mae     standard        2.22 Preprocessor1_Mo… <tibble>
 2 <split [35/4]> Fold02 mae     standard        2.34 Preprocessor1_Mo… <tibble>
 3 <split [35/4]> Fold03 mae     standard        2.56 Preprocessor1_Mo… <tibble>
 4 <split [35/4]> Fold04 mae     standard        1.51 Preprocessor1_Mo… <tibble>
 5 <split [35/4]> Fold05 mae     standard        1.81 Preprocessor1_Mo… <tibble>
 6 <split [35/4]> Fold06 mae     standard        2.43 Preprocessor1_Mo… <tibble>
 7 <split [35/4]> Fold07 mae     standard        1.61 Preprocessor1_Mo… <tibble>
 8 <split [35/4]> Fold08 mae     standard        1.84 Preprocessor1_Mo… <tibble>
 9 <split [35/4]> Fold09 mae     standard        1.28 Preprocessor1_Mo… <tibble>
10 <split [36/3]> Fold10 mae     standard        1.10 Preprocessor1_Mo… <tibble>
# b. fold 3 had the worst error (2.56)

# c. use these metrics to confirm the 1.87 CV MAE for model_1
model_1_cv %>% 
  unnest(.metrics) %>% 
  filter(.metric == "mae") %>% 
  summarize(mean(.estimate))
# A tibble: 1 × 1
  `mean(.estimate)`
              <dbl>
1              1.87


  1. Comparing models
Solution
  1. model_2
  2. model_1
  3. model_1 – model_2 produces bad predictions for new adults (and will also be hard to interpret!)
  4. model_1 is NOT overfit – its predictions of height for new adults seem roughly as accurate as the predictions for the adults in our sample. model_2 IS overfit – its predictions of height for new adults are worse than the predictions for the adults in our sample.


  1. LOOCV
Solution
  1. There are 39 people in our sample, thus LOOCV is equivalent to 39-fold CV:
nrow(humans)
model_1_loocv <- lm_spec %>% 
  fit_resamples(
    height ~ hip + weight + thigh + knee + ankle,
    resamples = vfold_cv(humans, v = nrow(humans)), # this will give an error and tell you to use loo_cv() instead, but conceptually this is the idea of how we'd do LOOCV
    metrics = metric_set(mae)
  )
    
model_1_loocv %>% 
  collect_metrics()
  1. There’s no randomness in the test folds. Each test fold is a single person.


  1. Data drill
Solution 
# a (one of many solutions)
humans %>% 
  mutate(younger_older = age < 40) %>% 
  group_by(younger_older) %>% 
  summarize(mean(height))
# A tibble: 2 × 2
  younger_older `mean(height)`
  <lgl>                  <dbl>
1 FALSE                   70.4
2 TRUE                    69.8
# b
humans %>% 
  filter(age >= 30) %>% 
  ggplot(aes(x = age, y = height)) + 
  geom_point()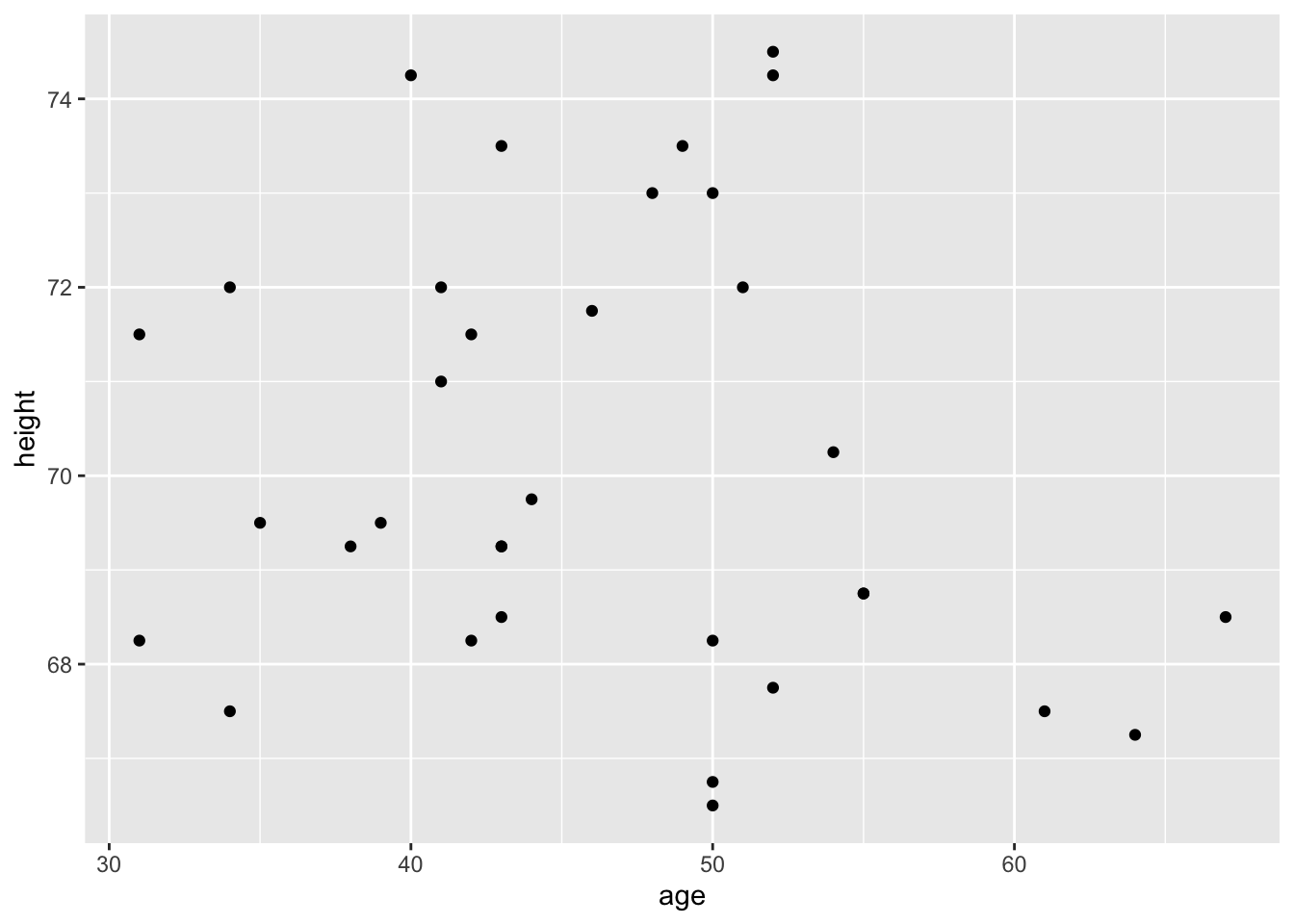

# c
model_3 <- lm_spec %>%
  fit(height ~ age, data = humans)
model_3 %>%
  tidy()
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  71.1       1.63      43.7   1.96e-33
2 age          -0.0210    0.0363    -0.577 5.67e- 1


  1. Reflection: Part 1
Solution Solutions will not be provided for this exercise. Review the course website, videos, checkpoints, homework assignments, etc. for this unit, and then stop by office hours if you’re having a hard time finding the answer to any of these questions!




Wrapping Up

Today’s Material

  • If you didn’t finish the exercises, no problem! Be sure to complete them outside of class, review the solutions on the course site, and ask any outstanding questions on Slack or in office hours.

  • This is the end of Unit 1, so there are reflection questions at the end of the exercises to help you organize the concepts in your mind. This is a good time to pause, review the material we’ve covered so far, and stop by office hours with any questions!

  • An R tutorial video, talking through the new code, is posted under the resources for today’s class on the Course Schedule (as well as an ISLR reading and two supplemental videos). Reviewing these resources is OPTIONAL. Decide what’s right for you.

Upcoming Deadlines

  • CP4:
    • due 10 minutes before our next class
    • covers one video
  • HW1:
    • due Friday at 11:59 pm
    • you have everything you need to finish this assignment after today’s class!
    • review the homework and late work/extension policies on Moodle/Syllabus: deadline is so we can get timely feedback to you; three 3-day extensions to acknowledge “life happens”

  1. https://www.wallpaperflare.com/grayscale-photography-of-guitar-headstock-music-low-electric-bass-wallpaper-zzbyn↩︎