3  Overfitting

Settling In

• Sit in your NEW randomly assigned group
• Introduce yourselves and choose a team name (you’ll need this later)
• Catch up on any Slack messages you might have missed
• Prepare to take notes:
  • Locate the QMDs for today’s activity (see the Course Schedule)
  • Save these documents in your “STAT 253 > Notes” folder
  • You can open the Part 1 QMD…
  • .. but DO NOT open Part 2 (yet)

Syllabus Highlights

Let’s review a few highlights from the Course Syllabus

• Course Structure
• Grading
• Preceptors / Office Hours
• Questions???

Small Group Discussion

To start class today, we’re going to do a Model Evaluation Experiment!

First, we’ll review some model evaluation ideas from last class.

Directions

Let’s build and evaluate a predicted model of an adult’s height (\(y\)) using some predictors \(x_i\) (e.g., age, weight, etc.).

• Introduce yourself in whatever way you feel appropriate and check in with each other as human beings
• Come up with a team name
• Work through the steps below as a group, after you are told your group number
  • Each group will be given a different sample of 40 adults
  • Start by predicting height (in) using hip circumference (cm)
  • Evaluate the model on your sample.
• Be prepared to share your answers to:
  • How good is your simple model?
  • What would happen if we added more predictors?

Questions

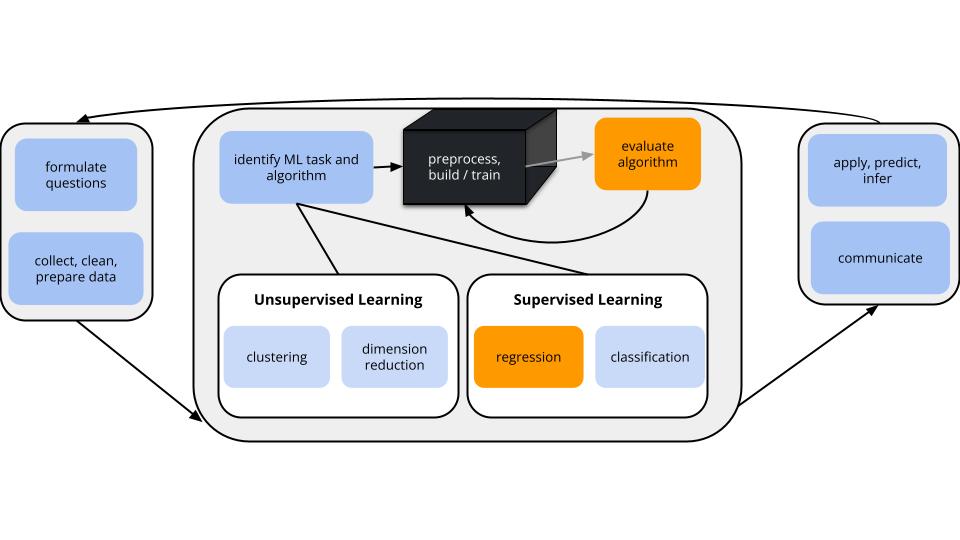
Goal

• Let’s build and evaluate a predictive model of an adult’s height (\(y\)) using some predictors \(x_i\) (eg: age, height, etc).

• Since \(y\) is quantitative this is a regression task.

• There are countless possible models of \(y\) vs \(x\). We’ll utilize a linear regression model:

\[y = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p + \varepsilon\]

• And after building this model, we’ll evaluate it.

Data: Each group will be given a different sample of 40 adults.

# Load packages needed for this analysis
library(tidyverse)
library(tidymodels)

Using the following starter code, fill in the blank in the URL with the appropriate number depending on your group number:

• Group 1: 50
• Group 2: 143
• Group 3: 86
• Group 4: 160
• Groups 5 & 6: 174

REMINDER: Do not edit the starter code directly. Instead, copy-paste the code into an empty code chunk below. Then, make edits (eg fill in blanks) in that second code chunk.

# Load data
humans <- read.csv("https://Mac-Stat.github.io/data/bodyfat___.csv") %>% 
  filter(ankle < 30) %>% 
  rename(body_fat = fatSiri)

Check out a density plot of your outcome:

# Plot data
ggplot(humans, aes(x = ___)) + 
  geom____()

Model building: Build a linear regression model of height (in) by hip circumference (cm).

# STEP 1: model specification
lm_spec <- ___() %>% 
  set_mode(___) %>% 
  set_engine(___)

# STEP 2: model estimation
model_1 <- ___ %>% 
  ___(height ~ hip, data = humans)

# Check out the coefficients
# Do all groups have the same coefficients? Should they?

Model evaluation: How good is our model?

# Calculate the R^2 for model_1

# Use your model to predict height for your subjects
# Just print the first 6 results
model_1 %>% 
  ___(new_data = ___) %>% 
  head()

# Calculate the MAE, i.e. typical prediction error, for your model
model_1 %>% 
  augment(new_data = humans) %>% 
  ___(truth = ___, estimate = ___)

Reflection

In addition to hip circumference, suppose we incorporated more predictors into our model of height. What would happen to \(R^2\)? To the MAE?

Exercises (Part 1)

Directions

• Take 5 minutes to complete exercises 1 and 2 (choosing one of three models).
• We’ll pause for a few minutes to discuss each group’s answers to these exercises.
• Then, and only then, you can finish exercises 3 - 5.

REMINDERS:

• Be kind to yourself/each other. You will make mistakes!
• Collaborate:
  • actively contribute to discussion (don’t work on your own)
  • actively include all group members in discussion
  • create a space where others feel comfortable making mistakes and sharing their ideas
  • stay in sync

Questions

1. Select a model

Consider 3 different models of height, estimated below. As a group, use your data to choose which is the best predictive model of height. Calculate the MAE for this model.

# height vs hip
model_1 <- lm_spec %>% 
  fit(height ~ hip, data = humans)

model_1 %>% 
  tidy()

# height vs hip & weight
model_2 <- lm_spec %>% 
  fit(height ~ hip + weight, data = humans)

model_2 %>% 
  tidy()

# height vs a lot of predictors (AND some interaction terms)
model_3 <- lm_spec %>% 
  fit(height ~ chest * age * weight * body_fat * abdomen + hip + thigh + knee + ankle + biceps + forearm + wrist, data = humans)

model_3 %>% 
  tidy()

# Calculate the MAE for your model
___ %>% 
  augment(new_data = humans) %>% 
  mae(truth = height, estimate = .pred)

2. Share your results
   Only when you’re done with exercise 1:
   • Open this “Top Model Competition” Google Doc.
   • Record your team name.
   • Record which model you chose (1, 2, or 3).
   • Record the MAE for your model.
   • WAIT. Don’t keep going.

Don’t peak

What do you know?! 40 new people just walked into the doctor’s office and the doctor wants to predict their height:

# Import the new data
new_patients <- read.csv("https://Mac-Stat.github.io/data/bodyfat182.csv") %>% 
  filter(ankle < 30) %>% 
  rename(body_fat = fatSiri)

3. Intuition
   Consider using your model to predict height for these 40 new subjects. On average, do you think these predictions will be better or worse than for your original patients? Why?

4. How well does your model do in the real world?
   Use your model to predict height for the new patients and calculate the typical prediction error (MAE). Record this in the Google sheet.

___ %>% 
  augment(new_data = new_patients) %>% 
  mae(truth = height, estimate = .pred)

5. Reflection
   In summary, which model seems best? What’s the central theme here?

Now open and save the QMD for Part 2.

Learning Goals

• Explain why training/in-sample model evaluation metrics can provide a misleading view of true test/out-of-sample performance
• Implement testing and training sets in R using the tidymodels package

Notes

Overfitting

When we add more and more predictors into a model, it can become overfit to the noise in our sample data:

• our model loses the broader trend / big picture
• thus does not generalize to new data
• thus results in bad predictions and a bad understanding of the relationship among the new data points

Preventing overfitting: training and testing

• In-sample metrics, i.e. measures of how well the model performs on the same sample data that we used to build it, tend to be overly optimistic and lead to overfitting.
• Instead, we should build and evaluate, or train and test, our model using different data.

R Code

Note

This section is for future reference. It is a summary of code you’ll learn below for creating and applying training and testing data. You don’t need to (and in fact should not) run the code in this section—just use this as example code for future reference.

Suppose we wish to build and evaluate a linear regression model of y vs x1 and x2 using our sample_data.

# Load packages
library(tidyverse)
library(tidymodels)

Split the sample data into training and test sets

# Set the random number seed
set.seed(___)

# Split the sample_data
# "prop" is the proportion of data assigned to the training set
# it must be some number between 0 and 1
data_split <- initial_split(sample_data, strata = y, prop = ___)

# Get the training data from the split
data_train <- data_split %>% 
  training()

# Get the testing data from the split
data_test <- data_split %>% 
  testing()

Build a training model

# STEP 1: model specification
lm_spec <- linear_reg() %>% 
  set_mode("regression") %>% 
  set_engine("lm")

# STEP 2: model estimation using the training data
model_train <- lm_spec %>% 
  fit(y ~ x1 + x2, data = data_train)

Use the training model to make predictions for the test data

# Make predictions
model_train %>% 
  augment(new_data = data_test)

Evaluate the training model using the test data

# Calculate the test MAE
model_train %>% 
  augment(new_data = data_test) %>% 
  mae(truth = y, estimate = .pred)

Exercises (Part 2)

Directions

• Open the Part 2 QMD file
• Same directions as before:
  • Be kind to yourself/each other
  • Collaborate
• We will not discuss these exercises as a class. Be sure to ask questions as I walk around the room.

Questions

The following exercises are inspired by Chapter 5.3.1 of ISLR.

# Load packages & data
# NOTE: You might first need to install the ISLR package
library(tidyverse)
library(tidymodels)
library(ISLR)
data(Auto)
cars <- Auto %>% 
  dplyr::select(mpg, horsepower, year)

Let’s use the cars data to compare three linear regression models of fuel efficiency in miles per gallon (mpg) by engine power (horsepower):

# Raw data
cars_plot <- ggplot(cars, aes(x = horsepower, y = mpg)) + 
  geom_point()
cars_plot

# model 1: 1 predictor (y = b0 + b1 x)
cars_plot + 
  geom_smooth(method = "lm", se = FALSE)

# model 2: 2 predictors (y = b0 + b1 x + b2 x^2)
cars_plot + 
  geom_smooth(method = "lm", se = FALSE, formula = y ~ poly(x, 2))

# model 3: 19 predictors (y = b0 + b1 x + b2 x^2 + ... + b19 x^19)
cars_plot + 
  geom_smooth(method = "lm", se = FALSE, formula = y ~ poly(x, 19))

Goal

Let’s evaluate and compare these models by training and testing them using different data.

1. 155 review: set.seed()

Run the two chunks below multiple times each. Afterward, summarize what set.seed() does and why it’s important to being able to reproduce a random sample.

sample_n(cars, 2)

set.seed(253)
sample_n(cars, 2)

 

2. Training and test sets

Let’s randomly split our original 392 sample cars into two separate pieces: select 80% of the cars to train (build) the model and the other 20% to test (evaluate) the model.

# Set the random number seed
set.seed(8)
    
# Split the cars data into 80% / 20%
# Ensure that the sub-samples are similar with respect to mpg
cars_split <- initial_split(cars, strata = mpg, prop = 0.8)

# Check it out
# What do these numbers mean?
cars_split

# Get the training data from the split
cars_train <- cars_split %>% 
  training()
    
# Get the testing data from the split
cars_test <- cars_split %>% 
  testing()

# The original data has 392 cars
nrow(cars)
    
# How many cars are in cars_train?
    
# How many cars are in cars_test?

3. Reflect on the above code

1. Why do we want the training and testing data to be similar with respect to mpg (strata = mpg)? What if they weren’t?
2. Why did we need all this new code instead of just using the first 80% of cars in the sample for training and the last 20% for testing?

4. Build the training model

# STEP 1: model specification
lm_spec <- linear_reg() %>% 
  set_mode("regression") %>% 
  set_engine("lm")

# STEP 2: model estimation using the training data
# Construct the 19th order polynomial model using the TRAINING data
model_19_train <- ___ %>% 
  ___(mpg ~ poly(horsepower, 19), data = ___)

5. Evaluate the training model

# How well does the TRAINING model predict the TRAINING data?
# Calculate the training (in-sample) MAE
model_19_train %>% 
  augment(new_data = ___) %>% 
  mae(truth = mpg, estimate = .pred)

# How well does the TRAINING model predict the TEST data?
# Calculate the test MAE
model_19_train %>% 
  augment(new_data = ___) %>% 
  mae(truth = mpg, estimate = .pred)

6. Punchline
   The table below summarizes your results for train_model_19 as well as the other two models of interest. (You should confirm the other two model results outside of class!)

Model	Training MAE	Testing MAE
mpg ~ horsepower	3.78	4.00
mpg ~ poly(horsepower, 2)	3.20	3.49
mpg ~ poly(horsepower, 19)	2.99	6.59

Answer the following and reflect on why each answer makes sense:

1. Within each model, how do the training errors compare to the testing errors? (This isn’t always the case, but is common.)
   
2. What about the training and test errors for the third model suggest that it is overfit to our sample data?
3. Which model seems the best with respect to the training errors?
   
4. Which model is the best with respect to the testing errors?
   
5. Which model would you choose?

7. Final reflection
   1. The training / testing procedure provided a more honest evaluation and comparison of our model predictions. How might we improve upon this procedure? What problems can you anticipate in splitting our data into 80% / 20%?
   2. Summarize the key themes from today in your own words.

8. STAT 155 REVIEW: data drill

1. Construct and interpret a plot of mpg vs horsepower and year.
2. Calculate the average mpg.
3. Calculate the average mpg for each year. HINT: group_by()
4. Plot the average mpg by year.

9. Digging deeper (optional)

Check out the online solutions for exercise 6. Instead of calculating MAE from scratch for 3 different models, I wrote a function calculate_MAE() to automate the process. After picking through this code, adapt the function so that it also returns the \(R^2\) value of each model.

Wrap-Up

Finishing the Activity

• If you didn’t finish the activity, no problem! Be sure to complete the activity outside of class, review the solutions in the online manual, and ask any questions on Slack or in office hours.
• Re-organize and review your notes to help deepen your understanding, solidify your learning, and make homework go more smoothly!

After Class

• An R code video, posted under the additional resources for today’s class (see the “Schedule” page on this website), talks through the new code.
  • This video is OPTIONAL. Decide what’s right for you.
• Continue to check in on Slack.
• Upcoming due dates:
  • CP3: due 10 minutes before our next class.
    • There are two (short) videos to watch in advance.
  • HW1 (Regression Model Evaluation): due next week
    • Start today, even if you just review the directions and scan the exercises. Homework is not designed to be completed in one sitting!
    • Invite others to work with you!
  • Stop by office hours (preceptors or mine) with any questions

Solutions

Small Group Discussion

Data

Solution

Each group will have slightly different plots because they have different samples of data.

Throughout the solutions I’ll use one of the datasets as an example:

humans <- read.csv("https://Mac-Stat.github.io/data/bodyfat50.csv") %>% 
  filter(ankle < 30) %>% 
  rename(body_fat = fatSiri)

ggplot(humans, aes(x = height)) + 
  geom_density()

Model building

Solution

Each group will have slightly different coefficients because they have different samples of data.

# STEP 1: model specification
lm_spec <- linear_reg() %>% 
  set_mode('regression') %>% 
  set_engine('lm')

# STEP 2: model estimation
model_1 <- lm_spec %>% 
  fit(height ~ hip, data = humans)

# Check out the coefficients
model_1  %>% 
  tidy()

# A tibble: 2 × 5
  term        estimate std.error statistic      p.value
  <chr>          <dbl>     <dbl>     <dbl>        <dbl>
1 (Intercept)   52.5      7.68        6.84 0.0000000460
2 hip            0.179    0.0778      2.30 0.0272      

Model evaluation

Solution

Again, each group will have slightly different answers here because they have different samples of data.

# Calculate the R^2 for model_1
model_1 %>%
  glance()

# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>   <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.125         0.101  2.26      5.29  0.0272     1  -86.1  178.  183.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

# Use your model to predict height for your subjects
# Just print the first 6 results
model_1 %>% 
  augment(new_data = humans) %>% 
  head()

# A tibble: 6 × 21
  .pred .resid fatBrozek body_fat density   age weight height adiposity
  <dbl>  <dbl>     <dbl>    <dbl>   <dbl> <int>  <dbl>  <dbl>     <dbl>
1  70.3  -1.09      24.7     25.4    1.04    43   177    69.2      26  
2  70.8  -1.52      22       22.5    1.05    38   187.   69.2      27.5
3  70.2  -1.19       9.4      8.8    1.08    29   161.   69        23.8
4  68.9   4.58       7.1      6.3    1.08    49   153.   73.5      19.9
5  69.3   2.91       9.9      9.4    1.08    23   160.   72.2      21.6
6  70.2  -2.48      22.7     23.3    1.05    52   167    67.8      25.6
# ℹ 12 more variables: fatFreeWeight <dbl>, neck <dbl>, chest <dbl>,
#   abdomen <dbl>, hip <dbl>, thigh <dbl>, knee <dbl>, ankle <dbl>,
#   biceps <dbl>, forearm <dbl>, wrist <dbl>, hipin <dbl>

# Calculate the MAE, i.e. typical prediction error, for your model
model_1 %>% 
  augment(new_data = humans) %>% 
  mae(truth = height, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard        1.88

Reflection

Solution

\(R^2\) would increase and MAE would decrease.

Exercises (Part 1)

1. Select a model

Solution

Will vary by group. MAE is calculated here for each model.

# Build the models
model_1 <- lm_spec %>% 
  fit(height ~ hip, data = humans)
model_2 <- lm_spec %>% 
  fit(height ~ hip + weight, data = humans)
model_3 <- lm_spec %>% 
  fit(height ~ chest * age * weight * body_fat * abdomen + hip + thigh + knee + ankle + biceps + forearm + wrist, data = humans)

# Evaluate the models
model_1 %>% 
  augment(new_data = humans) %>% 
  mae(truth = height, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard        1.88

model_2 %>% 
  augment(new_data = humans) %>% 
  mae(truth = height, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard        1.67

model_3 %>% 
  augment(new_data = humans) %>% 
  mae(truth = height, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard    1.53e-10

2. Share your results.

Solution

Done! (Model 3 had the best MAE for this dataset.)

3. Intuition.

Solution

Answers will vary.

4. How well does your model do in the real world?

Solution

# Predict height (assume, for example, I choose model_1)
model_1 %>% 
  augment(new_data = new_patients) %>% 
  head()

# A tibble: 6 × 21
  .pred .resid fatBrozek body_fat density   age weight height adiposity
  <dbl>  <dbl>     <dbl>    <dbl>   <dbl> <int>  <dbl>  <dbl>     <dbl>
1  71.5 -1.96       27.1     28      1.04    62   201.   69.5      29.3
2  70.4 -0.141      20.9     21.3    1.05    42   163    70.2      23.3
3  69.7 -0.497      26.1     27      1.04    72   168    69.2      24.7
4  69.1 -1.39        4.1      3      1.09    35   152.   67.8      23.4
5  68.5 -2.99        1.9      0.7    1.1     35   126.   65.5      20.6
6  71.9 -1.91       31       32.3    1.03    57   206.   70        29.5
# ℹ 12 more variables: fatFreeWeight <dbl>, neck <dbl>, chest <dbl>,
#   abdomen <dbl>, hip <dbl>, thigh <dbl>, knee <dbl>, ankle <dbl>,
#   biceps <dbl>, forearm <dbl>, wrist <dbl>, hipin <dbl>

# Calculate the MAE for model_1
model_1 %>% 
  augment(new_data = new_patients) %>% 
  mae(truth = height, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard        1.73

# Calculate the MAE for model_2
model_2 %>% 
  augment(new_data = new_patients) %>% 
  mae(truth = height, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard        1.68

# Calculate the MAE for model_3
model_3 %>% 
  augment(new_data = new_patients) %>% 
  mae(truth = height, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard        105.

5. Reflection

Solution

A few takeaways:

• In general, models tend to perform worse on new data then on the data on which they were built/trained
• In this particular example, Model 2 looks best on new data, and Model 3 performs horribly.
• Model 3 is overfit to the training data. This is more likely to happen with an overly complicated model.

Exercises (Part 2)

1. 155 review: set.seed()

Solution

set.seed() is used to create the same “random numbers” each time a random function is called.

Note that is if you want to get exactly the same random result, set.seed() needs to be run right before the call to random function, every time.

It is important so that you can reproduce the same random sample every time you knit your work.

There might be different results across computers/platforms as they might be using different pseudo-random number generators. The most important thing is for your code to be consistent.

2. Training and test sets

Solution

# Set the random number seed
set.seed(8)

# Split the cars data into 80% / 20%
# Ensure that the sub-samples are similar with respect to mpg
cars_split <- initial_split(cars, strata = mpg, prop = 0.8)

# Check it out
cars_split

<Training/Testing/Total>
<312/80/392>

# Get the training data from the split
cars_train <- cars_split %>% 
  training()

# Get the testing data from the split
cars_test <- cars_split %>% 
  testing()

# The original data has 392 cars
nrow(cars)

[1] 392

# How many cars are in cars_train?
nrow(cars_train)

[1] 312

# How many cars are in cars_test?
nrow(cars_test)

[1] 80

3. Reflect on the above code

Solution

1. Suppose, for example, the training cars all had higher mpg than the test cars. Then the training model likely would not perform well on the test cars, thus we’d get an overly pessimistic measure of model quality.
2. If the cars are ordered in some way (eg: from biggest to smallest) then our training and testing samples would have systematically different properties.

4. Build the training model

Solution

# STEP 1: model specification
lm_spec <- linear_reg() %>% 
  set_mode("regression") %>% 
  set_engine("lm")

# STEP 2: model estimation using the training data
# Construct the 19th order polynomial model using the TRAINING data
model_19_train <- lm_spec %>% 
  fit(mpg ~ poly(horsepower, 19), data = cars_train)

5. Evaluate the training model

Solution

# How well does the training model predict the training data?
# Calculate the training (in-sample) MAE
model_19_train %>% 
  augment(new_data = cars_train) %>% 
  mae(truth = mpg, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard        2.99

# How well does the training model predict the test data?
# Calculate the test MAE
model_19_train %>% 
  augment(new_data = cars_test) %>% 
  mae(truth = mpg, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard        6.59

6. Punchline

Solution

1. the training errors are smaller
   
2. the test MAE is much larger than the training MAE
3. the 19th order polynomial
   
4. the quadratic
   
5. the quadratic

Code for the curious

I wrote a function calculate_MAE() to automate the calculations in the table. If you’re curious, pick through this code!

# Write function to calculate MAEs
calculate_MAE <- function(poly_order){
  # Construct a training model
  model <- lm_spec %>% 
    fit(mpg ~ poly(horsepower, poly_order), cars_train)
  
  # Calculate the training MAE
  train_it <- model %>% 
    augment(new_data = cars_train) %>% 
    mae(truth = mpg, estimate = .pred)
      
  # Calculate the testing MAE
  test_it <- model %>% 
    augment(new_data = cars_test) %>% 
    mae(truth = mpg, estimate = .pred)
      
  # Return the results
  return(data.frame(train_MAE = train_it$.estimate, test_MAE = test_it$.estimate))
}
    
# Calculate training and testing MSEs
calculate_MAE(poly_order = 1)

  train_MAE test_MAE
1  3.779331 4.004333

calculate_MAE(poly_order = 2)

  train_MAE test_MAE
1  3.199882 3.487022

calculate_MAE(poly_order = 19)

  train_MAE test_MAE
1  2.989305 6.592341

# For those of you interested in trying all orders...

results <- purrr::map_df(1:19,calculate_MAE) %>% 
  mutate(order = 1:19) %>%
  pivot_longer(cols=1:2,names_to='Metric',values_to = 'MAE') 

results %>%
  ggplot(aes(x = order, y = MAE, color = Metric)) + 
  geom_line() + 
  geom_point(data = results %>% filter(Metric == 'test_MAE') %>% slice_min(MAE)) + 
  geom_point(data = results %>% filter(Metric == 'train_MAE') %>% slice_min(MAE))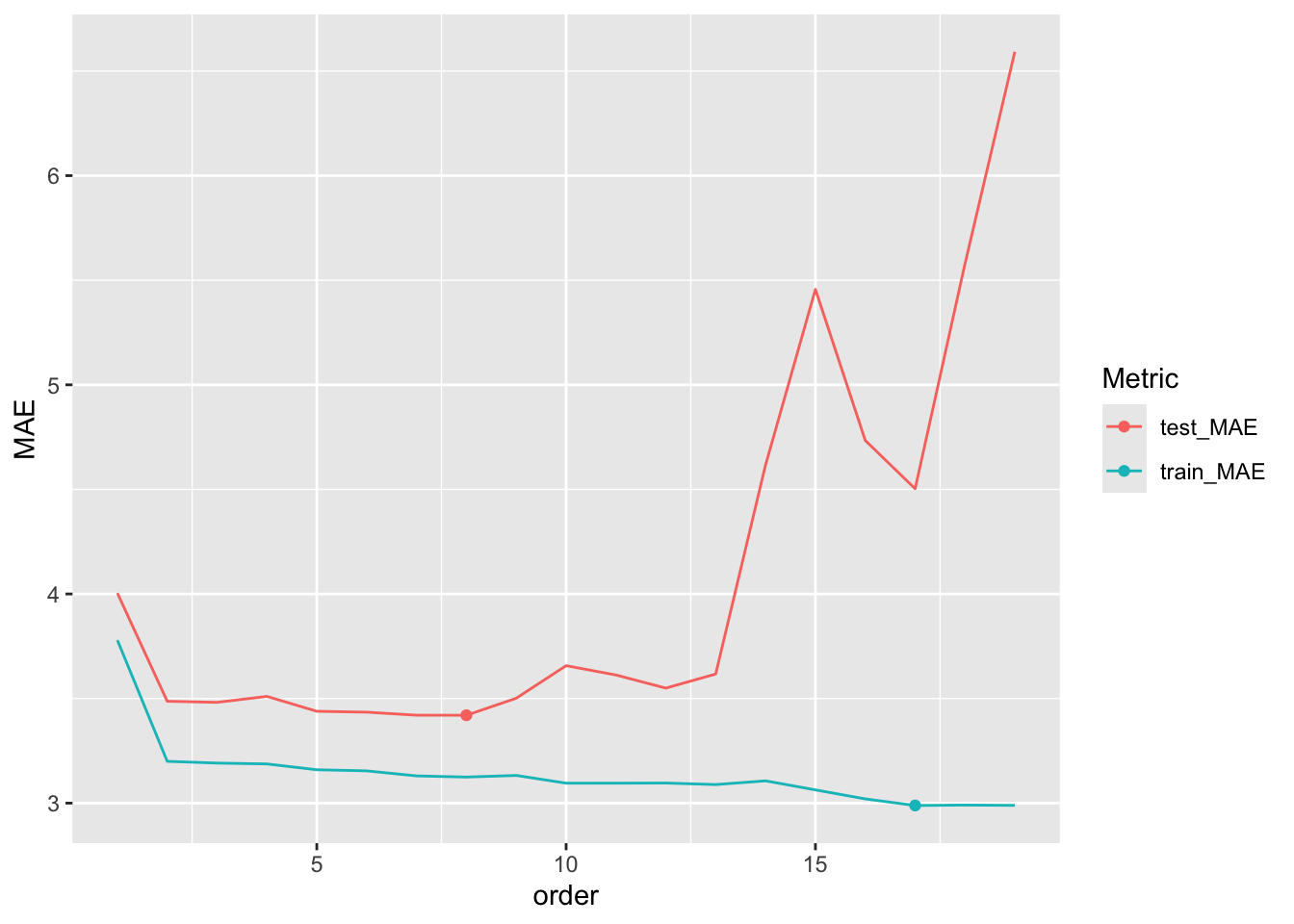

7. Final reflection

Solution

This will be discussed in the next video!

8. STAT 155 REVIEW: data drill

Solution

# a. One of many options
ggplot(cars, aes(x = horsepower, y = mpg, color = year)) + 
  geom_point()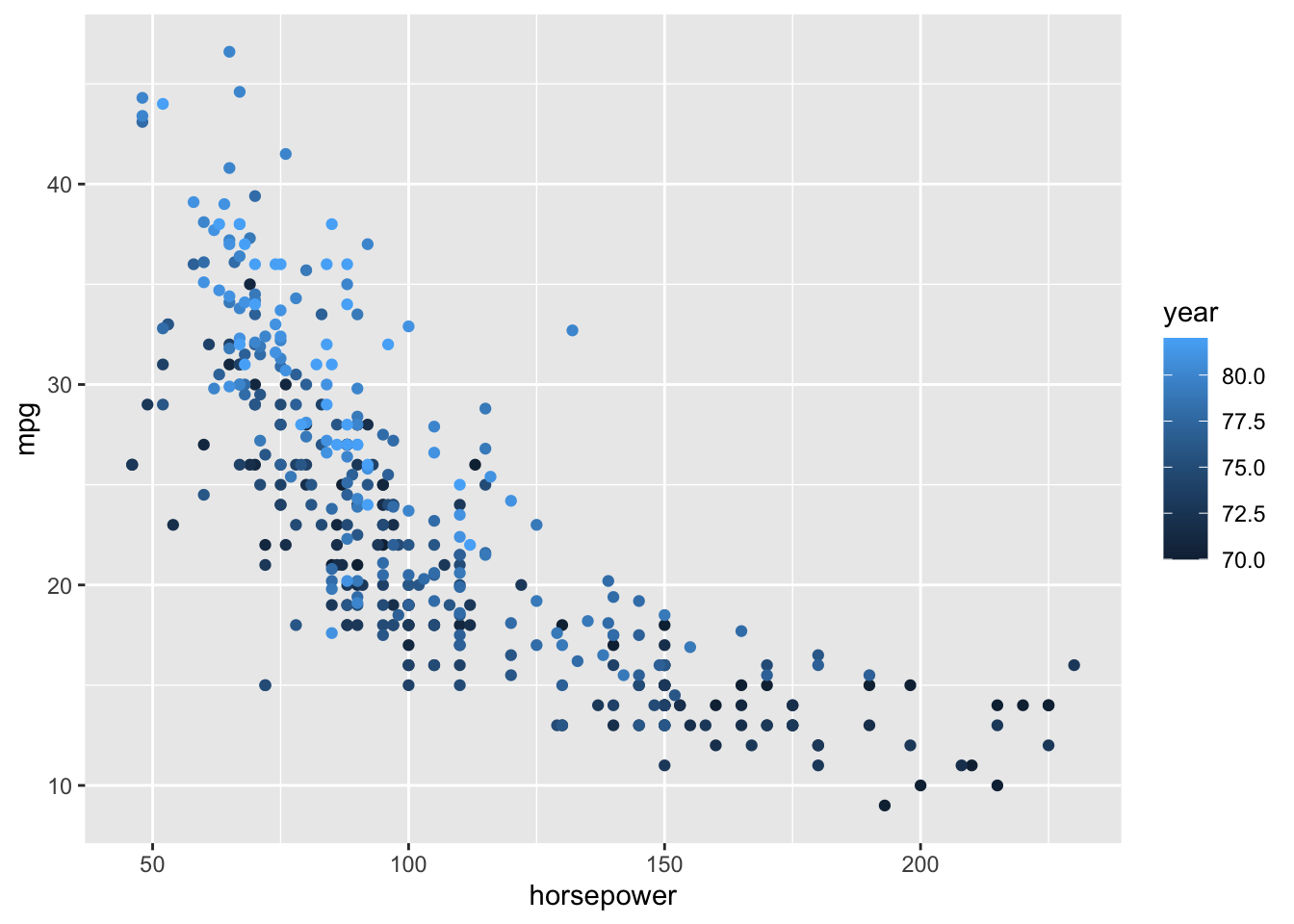

# b
cars %>% 
  summarize(mean(mpg))

  mean(mpg)
1  23.44592

# c
cars %>% 
  group_by(year) %>% 
  summarize(mean_mpg = mean(mpg))

# A tibble: 13 × 2
    year mean_mpg
   <dbl>    <dbl>
 1    70     17.7
 2    71     21.1
 3    72     18.7
 4    73     17.1
 5    74     22.8
 6    75     20.3
 7    76     21.6
 8    77     23.4
 9    78     24.1
10    79     25.1
11    80     33.8
12    81     30.2
13    82     32  

# d
cars %>% 
  group_by(year) %>% 
  summarize(mean_mpg = mean(mpg)) %>% 
  ggplot(aes(y = mean_mpg, x = year)) + 
  geom_point()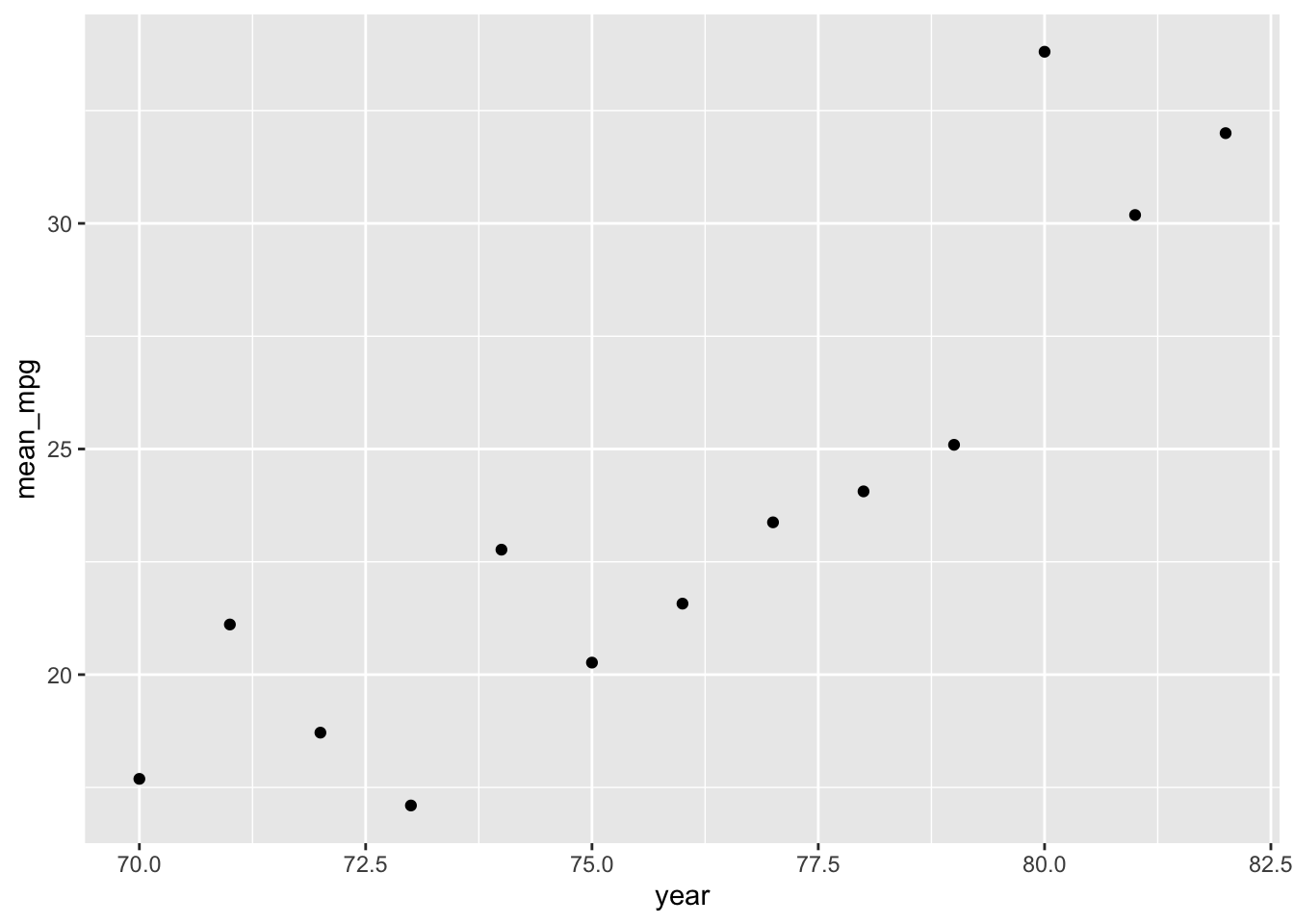

9. Digging deeper (optional)

Solution

Come chat in office hours :)