library(palmerpenguins)
data("penguins")
penguins %>%
select(bill_length_mm, bill_depth_mm, body_mass_g) %>%
head()18 Hierarchical Clustering
Settling In
- Sit wherever you want!
- Prepare to take notes (find the QMD for today in the usual spot)
- Catch up on any announcements you’ve missed on Slack
- Fill out the Group Assignment Feedback Survey (Moodle > Surveys)
- Please be specific when specifying who you want to work with for the next group assignment
Registration Tips
Thinking about what MSCS course to take next semester? Consider the following:
- Interested in working with data (eg wrangling, plotting, data acquisition, advanced data processing)? Try:
- COMP/STAT 112 (Intro to Data Science)
- COMP/STAT 212 (Intermediate Data Science)
- Interested in data and society? Apply to be part of this pilot class:
- STAT 202 (2-credit Data and Society)
- Interested in developing a mathematical foundation for better/deeper understanding of statistical methodology? Try:
- MATH/STAT 354 (Probability)
- STAT 452 (Correlated Data)
- Interested in learning some computing techniques that are fundamental to data science? Try:
- COMP 123 (Core Concepts in Comp Sci)
- COMP 127 (Object-Oriented Programming and Abstraction)
NOTE: all of the highlighted courses above require permission of instructor to register. Fill out the corresponding interest form by April 16th if you’re interested in taking any of these courses: https://www.macalester.edu/mscs/mscs-course-waitlists/
Learning Goals
- Clearly describe / implement by hand the hierarchical clustering algorithm
- Compare and contrast k-means and hierarchical clustering in their outputs and algorithms
- Interpret cuts of the dendrogram for single and complete linkage
- Describe the rationale for how clustering algorithms work in terms of within-cluster variation
- Describe the tradeoff of more vs. less clusters in terms of interpretability
- Implement strategies for interpreting / contextualizing the clusters
Notes: Unsupervised Learning
Context
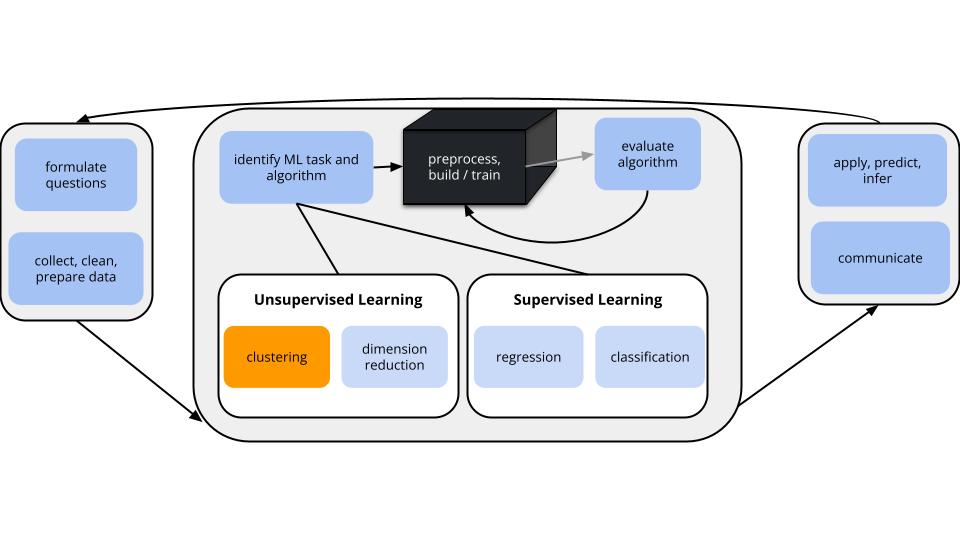
GOALS
Suppose we have a set of feature variables \((x_1,x_2,...,x_k)\) but NO outcome variable \(y\).
Instead of our goal being to predict/classify/explain \(y\), we might simply want to…
- Examine the structure of our data.
- Utilize this examination as a jumping off point for further analysis.
Unsupervised Methods
Cluster Analysis (Unit 6):
- Focus: Structure among the rows, i.e. individual cases or data points.
- Goal: Identify and examine clusters or distinct groups of cases with respect to their features x.
- Methods: hierarchical clustering & K-means clustering
Dimension Reduction (Unit 7):
- Focus: Structure among the columns, i.e. features x.
- Goal: Combine groups of correlated features x into a smaller set of uncorrelated features which preserve the majority of information in the data. (We’ll discuss the motivation later!)
- Methods: Principal components
Examples
Remember this from the first day of class?
For more examples, check out the Unit 6 Motivating Question page here.
Notes: Hierarchical Cluster Analysis
Let’s recap the main ideas from the videos you watched before class today.
Goal
Create a hierarchy of clusters where clusters consist of similar data points.
Algorithm
Suppose we have a set of p feature variables (\(x_1, x_2,..., x_p\)) on each of n data points. Each data point starts as a leaf.
- Compute the Euclidean distance between all pairs of data points with respect to x.
- Fuse the 2 closest data points into a single cluster or branch.
- Continue to fuse the 2 closest clusters until all cases are in 1 cluster.
NOTE: This is referred to as an “agglomerative” algorithm.
Dendrograms
The hierarchical clustering algorithm produces a dendrogram (of or relating to trees).
To use a dendrogram:
- Start with the leaves at the bottom (unlike classification trees!). Each leaf represents a single case / row in our dataset.
- Moving up the tree, fuse similar leaves into branches, fuse similar branches into bigger branches, fuse all branches into one big trunk (all cases).
- The more similar two cases, the sooner their branches will fuse. The height of the first fusion between two cases’ branches measures the “distance” between them.
- The horizontal distance between 2 leaves does not reflect distance!
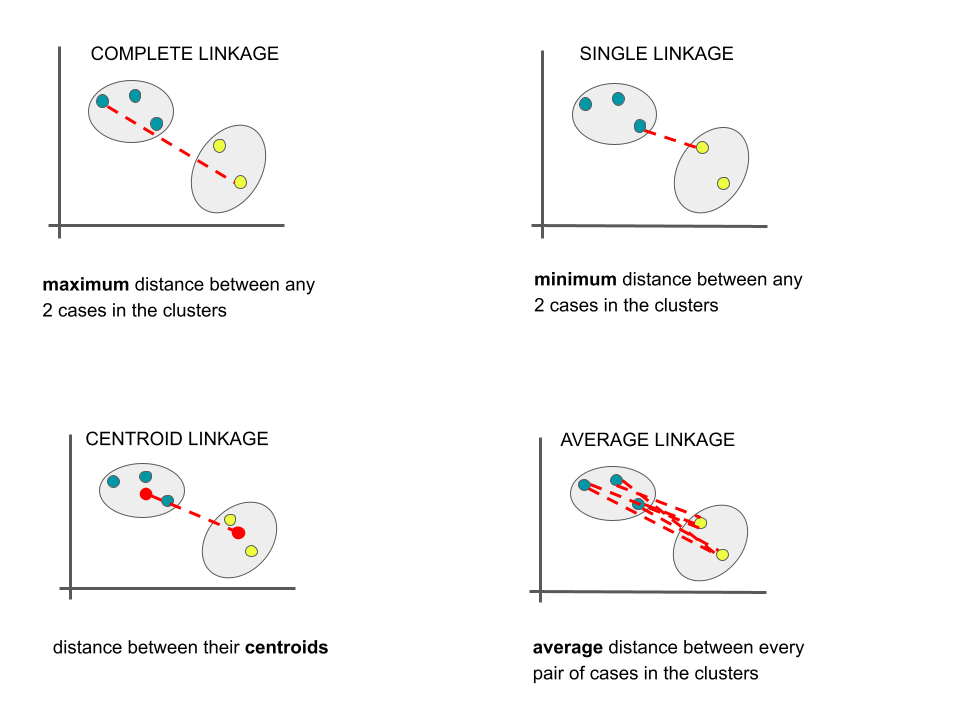
Measuring Distance
There are several linkages we can use to measure distance between 2 clusters / branches. Unless specified otherwise, we’ll use the complete linkage method.
Small Group Discussion
EXAMPLE 1: Standardizing the features
Let’s start by using hierarchical clustering to identify similar groups (and possible species!) of penguins with respect to their bill lengths (mm), bill depths (mm), and body masses (g).
This algorithm relies on calculating the distances between each pair of penguins.
Why is it important to first standardize our 3 features to the same scale (centered around a mean of 0 with standard deviation 1)?
EXAMPLE 2: Interpreting a dendrogram
Check out the standardized data, heat map, and dendrogram for a sample of just 50 penguins.
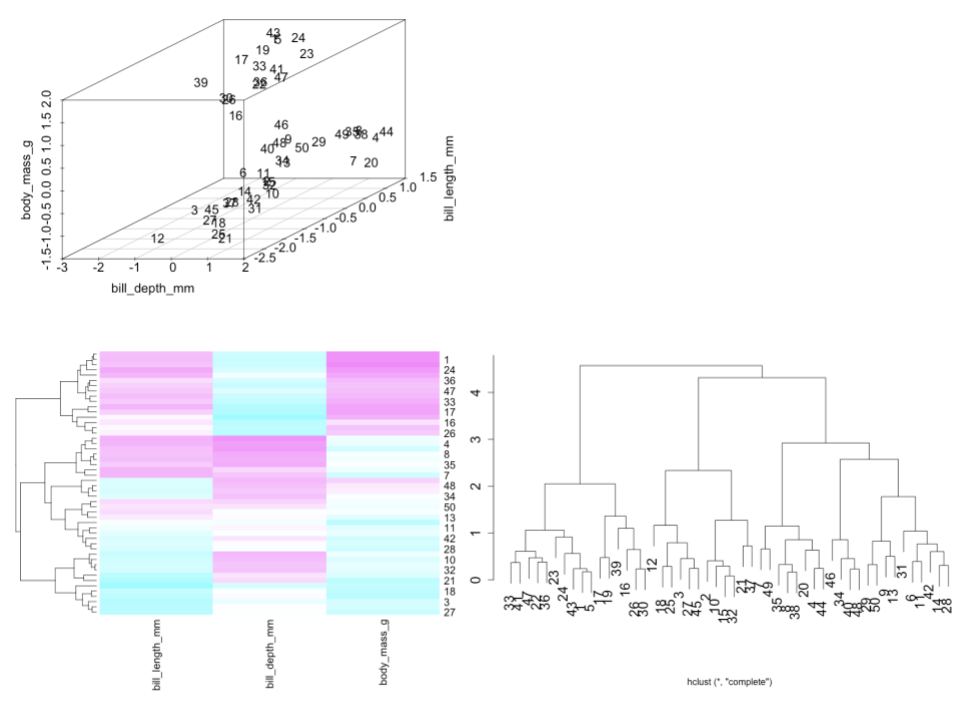
Is penguin 30 more similar to penguin 33 or 12?
Identify and interpret the distance, calculated using the complete linkage, between penguins 30 and 33.
Consider the far left penguin cluster on the dendrogram, starting with penguin 33 and ending with penguin 30. Use the heat map to describe what these penguins have in common.
EXAMPLE 3: By Hand
To really get the details, you’ll perform hierarchical clustering by hand for a small example.
Ask you instructor for a copy of the paper handout.
Code for importing the data is here:
# Record the data
penguins_small <- data.frame(
width = c(-1.3, -0.8, 0.2, 0.8, 1.0),
length = c(0.6, 1.4, -1.0, -0.2, -0.7))
# Plot the data
ggplot(penguins_small, aes(x = width, y = length)) +
geom_point() +
geom_text(aes(label = c(1:5)), vjust = 1.5) +
theme_minimal()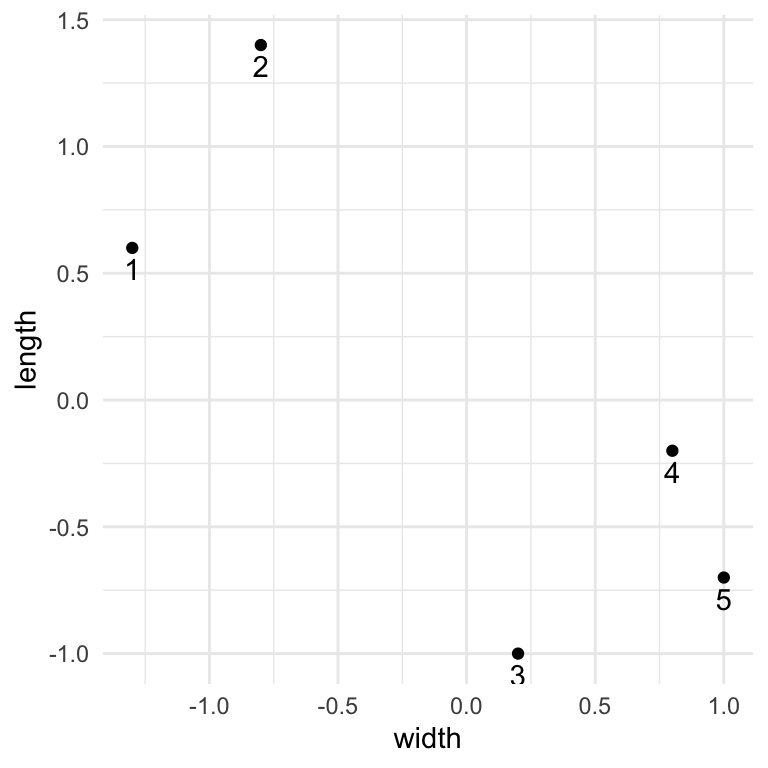
# Calculate the distance between each pair of penguins
round(dist(penguins_small), 2) 1 2 3 4
2 0.94
3 2.19 2.60
4 2.25 2.26 1.00
5 2.64 2.77 0.85 0.54# Type out the R code from Part b belowEXAMPLE 4: Explore Clusters
Now, let’s go back to a sample of 50 penguins.
Run the 2 chunks below to build a shiny app that we’ll use to build some intuition for hierarchical clustering.
Put the slider at 9 clusters. These 9 clusters are represented in the dendrogram and scatterplot of the data. Do you think that 9 clusters is too many, too few, or just right?
Now set the slider to 5. Simply take note of how the clusters appear in the data.
Now sloooooowly set the slider to 4, then 3, then 2. Each time, notice what happens to the clusters in the data plot. Describe what you observe.
What are your thoughts about the 2-cluster solution? What happened?!
Code
# Load the data
library(tidyverse)
set.seed(253)
more_penguins <- penguins %>%
sample_n(50) %>%
select(bill_length_mm, bill_depth_mm) %>%
na.omit()
# Run hierarchical clustering
penguin_cluster <- hclust(dist(scale(more_penguins)), method = "complete")
# Record cluster assignments
clusters <- more_penguins %>%
mutate(k = rep(1, nrow(more_penguins)), cluster = rep(1, nrow(more_penguins)))
for(i in 2:12){
clusters <- more_penguins %>%
mutate(k = rep(i, nrow(more_penguins)),
cluster = cutree(penguin_cluster, k = i)) %>%
bind_rows(clusters)
}Code
library(shiny)
library(factoextra)
library(RColorBrewer)
# Build the shiny server
server_hc <- function(input, output) {
dend_plot <- reactive({
cols = brewer.pal(n= input$k_pick, "Set1")
fviz_dend(penguin_cluster, k = input$k_pick, k_colors = cols)
})
output$model_plot <- renderPlot({
cols = brewer.pal(n= input$k_pick, "Set1")
dend <- attributes(dend_plot())$dendrogram
tree_order <- order.dendrogram(dend)
clusters_k <- clusters %>%
filter(k == input$k_pick)
clusters_k <- clusters_k %>%
mutate(cluster = factor(cluster, levels = unique(clusters_k$cluster[tree_order])))
names(cols) = unique(clusters_k$cluster[tree_order])
clusters_k %>%
ggplot(aes(x = bill_length_mm, y = bill_depth_mm, color = factor(cluster))) +
geom_point(size = 3) +
scale_color_manual(values = cols) +
theme_minimal() +
theme(legend.position = "none")
})
output$dendrogram <- renderPlot({
dend_plot()
})
}
# Build the shiny user interface
ui_hc <- fluidPage(
sidebarLayout(
sidebarPanel(
h4("Pick the number of clusters:"),
sliderInput("k_pick", "cluster number", min = 1, max = 9, value = 9, step = 1, round = TRUE)
),
mainPanel(
plotOutput("dendrogram"),
plotOutput("model_plot")
)
)
)
# Run the shiny app!
shinyApp(ui = ui_hc, server = server_hc)EXAMPLE 5: Details
Is hierarchical clustering greedy?
We learned in the video that, though they both produce tree-like output, the hierarchical clustering and classification tree algorithms are not the same thing! Similarly, though they both calculate distances between each pair of data points, the hierarchical clustering and KNN algorithms are not the same thing! Explain.
Note: When all features x are quantitative or logical (TRUE/FALSE), we measure the similarity of 2 data points with respect to the Euclidean distance between their standardized x values. But if at least 1 feature x is a factor / categorical variable, we measure the similarity of 2 data points with respect to their Gower distance. The idea is similar to what we did in KNN (converting categorical x variables to dummies, and then standardizing), but the details are different.
If you’re interested:
library(cluster)
?daisy
Exercises
For the rest of class, work together exercises 1-3 on HW6. We’ll cover material in the next class to complete the rest of the exercises.
Future Reference
Notes: R code
The tidymodels package is built for models of some outcome variable y. We can’t use it for clustering.
Instead, we’ll use a variety of new packages that use specialized, but short, syntax.
Suppose we have a set of sample_data with multiple feature columns x, and (possibly) a column named id which labels each data point.
# Install packages
library(tidyverse)
library(cluster) # to build the hierarchical clustering algorithm
library(factoextra) # to draw the dendrograms
PROCESS THE DATA
If there’s a column that’s an identifying variable or label, not a feature of the data points, convert it to a row name.
sample_data <- sample_data %>%
column_to_rownames("id")
RUN THE CLUSTERING ALGORITHM
# Scenario 1: ALL features x are quantitative OR logical (TRUE/FALSE)
# Use either a "complete", "single", "average", or "centroid" linkage_method
hier_model <- hclust(dist(scale(sample_data)), method = ___)
# Scenario 2: AT LEAST 1 feature x is a FACTOR (categorical)
# Use either a "complete", "single", "average", or "centroid" linkage
hier_model <- hclust(daisy(sample_data, metric = "gower"), method = ___)
VISUALIZING THE CLUSTERING: HEAT MAPS AND DENDRODGRAMS
NOTE: Heat maps can be goofy if at least 1 x feature is categorical
# Heat maps: ordered by the id variable (not clustering)
heatmap(scale(data.matrix(sample_data)), Colv = NA, Rowv = NA)
# Heat maps: ordered by dendrogram / clustering
heatmap(scale(data.matrix(sample_data)), Colv = NA)
# Dendrogram (change font size w/ cex)
fviz_dend(hier_model, cex = 1)
fviz_dend(hier_model, horiz = TRUE, cex = 1) # Plot the dendrogram horizontally to read longer labels
DEFINING & PLOTTING CLUSTER ASSIGNMENTS
# Assign each sample case to a cluster
# You specify the number of clusters, k
# We typically want to store this in a new dataset so that the cluster assignments aren't
# accidentally used as features in a later analysis!
cluster_data <- sample_data %>%
mutate(hier_cluster_k = as.factor(cutree(hier_model, k = ___)))
# Visualize the clusters on the dendrogram (change font size w/ cex)
fviz_dend(hier_model, k = ___, cex = 1)
fviz_dend(hier_model, k = ___, horiz = TRUE, cex = 1) # Plot the dendrogram horizontally to read longer labels
Wrapping Up
- As usual, take time after class to finish any remaining exercises, check solutions, reflect on key concepts from today, and come to office hours with questions
- Upcoming due dates:
- CP13: before next class (April 17)
- Quiz 2 Revisions: bring to class next Tuesday (April 22)
- HW6: end-of-day next Tuesday (April 22)
Solutions
Small Group Discussion
EXAMPLE 1: Standardizing the features
Solution:
The features are on different scales. It’s important to standardize so that one feature doesn’t have more influence over the distance measure, simply due to its scale.EXAMPLE 2: Interpreting a dendrogram
Solution:
- 33 – 30 and 33 cluster together sooner than 30 and 12
- This clustering was done using the complete linkage method. Thus at most, the standardized difference in the bill length, bill depth, and body mass of penguins 30 and 33 is 2.
- That group generally has large bill length and body mass but small bill depth.
EXAMPLE 3: By Hand
Solution:
COMPLETE LINKAGE
library(tree)
penguin_cluster <- hclust(dist(penguins_small), method = "complete")
plot(penguin_cluster)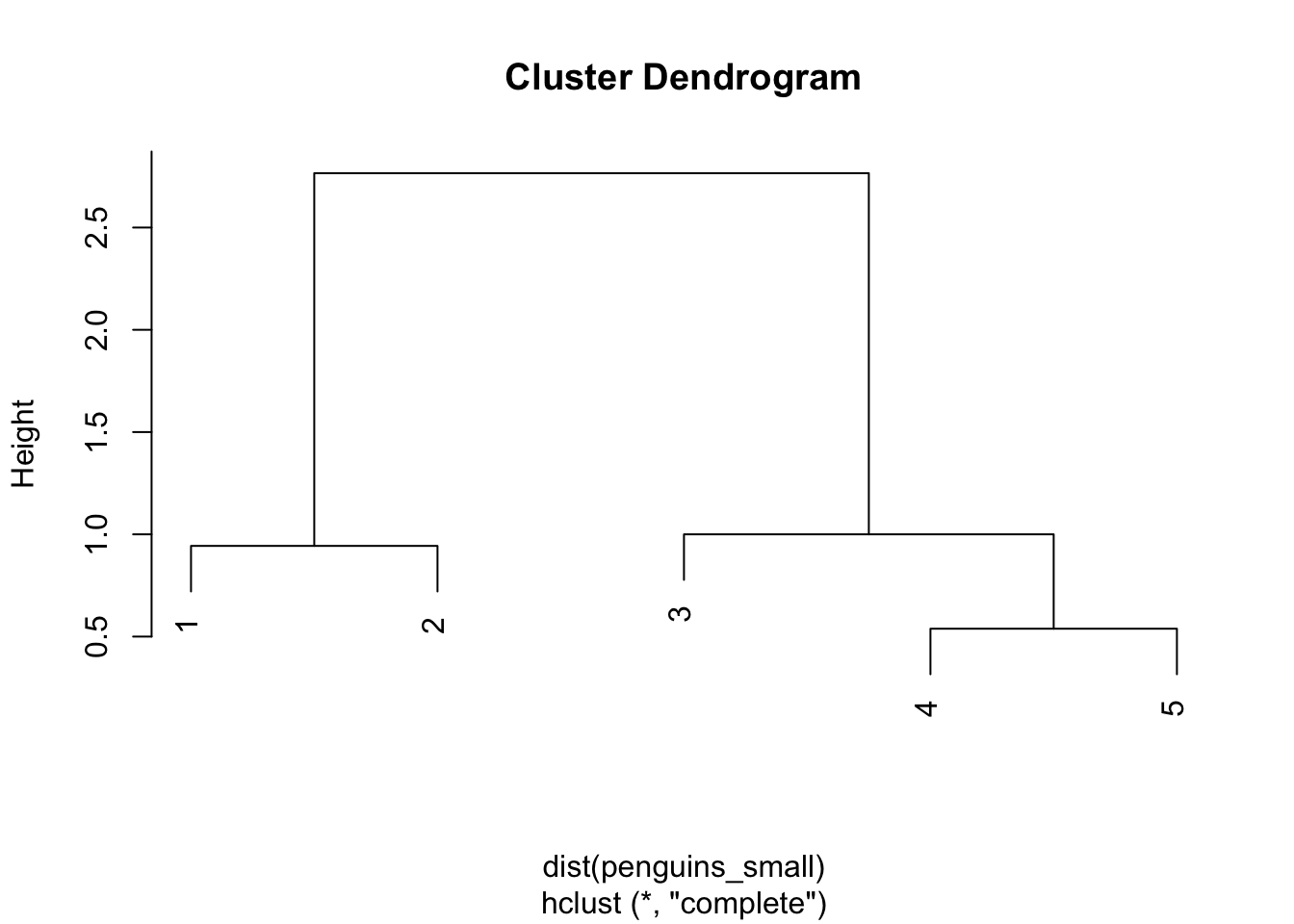
Step 1
The closest pair are 4 and 5 with a distance of 0.54
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | ||||
| 2 | 0.94 | 0 | |||
| 3 | 2.19 | 2.60 | 0 | ||
| 4 | 2.25 | 2.26 | 1.00 | 0 | |
| 5 | 2.64 | 2.77 | 0.85 | 0.54 | 0 |
Step 2
The distance matrix below gives the current distance between clusters 1, 2, 3, and (4 & 5) using complete linkage (the distance between 2 clusters is the maximum distance btwn any pair of penguins in the 2 clusters). By this, clusters or penguins 1 & 2 are the closest, with a distance of 0.94:
| 1 | 2 | 3 | 4 & 5 | |
|---|---|---|---|---|
| 1 | 0 | |||
| 2 | 0.94 | 0 | ||
| 3 | 2.19 | 2.60 | 0 | |
| 4 & 5 | 2.64 | 2.77 | 1.00 | 0 |
Step 3
The distance matrix below gives the current distance between clusters (1 & 2), 3, and (4 & 5) using complete linkage. By this, clusters 3 and (4 & 5) are the closest, with a distance of 1:
| 1 & 2 | 3 | 4 & 5 | |
|---|---|---|---|
| 1 & 2 | 0 | ||
| 3 | 2.60 | 0 | |
| 4 & 5 | 2.77 | 1.00 | 0 |
Step 4
The distance matrix below gives the current distance between our 2 clusters, (1 & 2) and (3 & 4 & 5) using complete linkage. The distance between them is 2.77 (hence the height of the final merge in our dendrogram):
| 1 & 2 | 3,4,5 | |
|---|---|---|
| 1 & 2 | 0 | |
| 3,4,5 | 2.77 | 0 |
SINGLE LINKAGE
penguin_cluster <- hclust(dist(penguins_small), method = "single")
plot(penguin_cluster)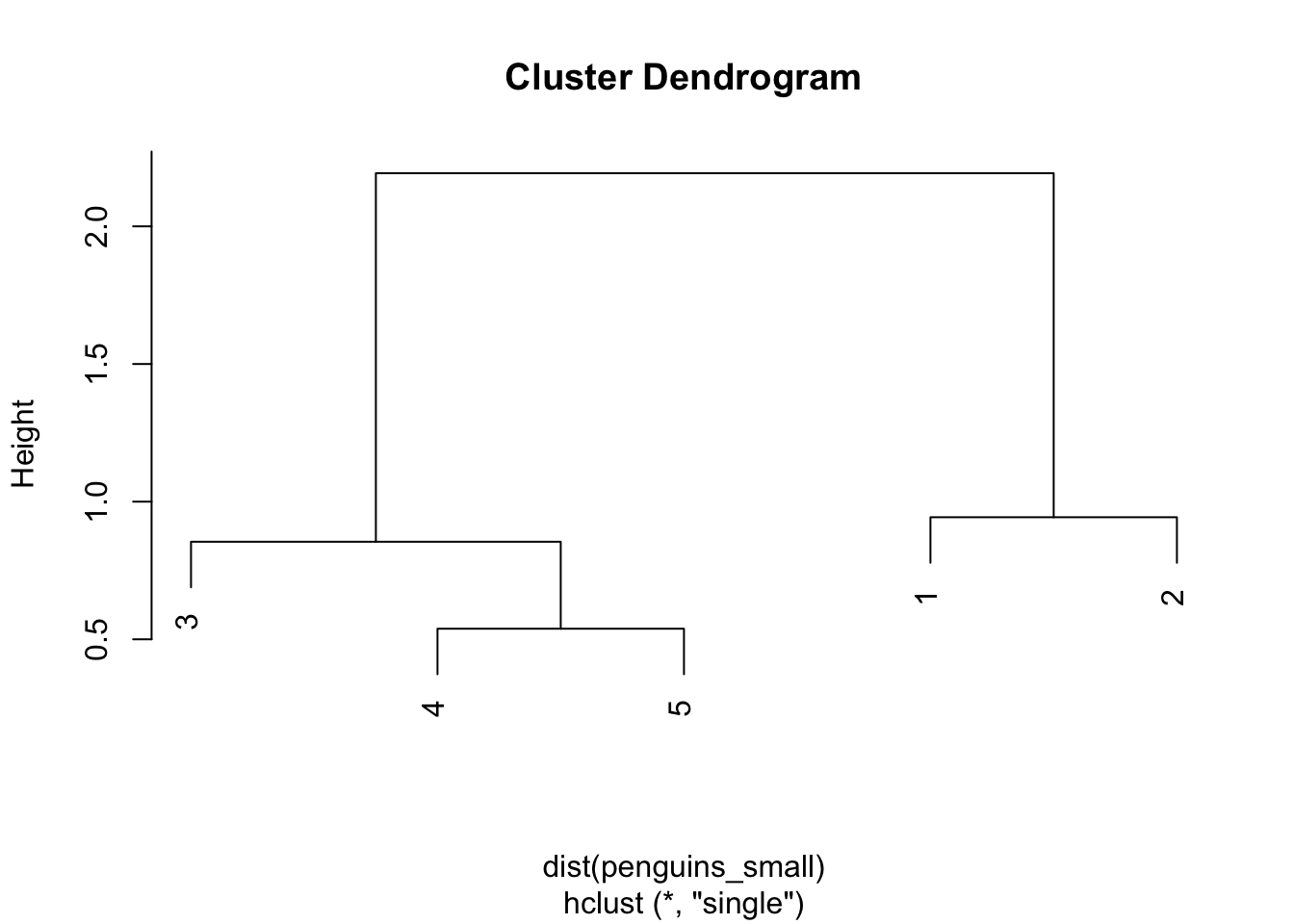
Step 1
The closest pair are 4 and 5 with a distance of 0.54
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | ||||
| 2 | 0.94 | 0 | |||
| 3 | 2.19 | 2.60 | 0 | ||
| 4 | 2.25 | 2.26 | 1.00 | 0 | |
| 5 | 2.64 | 2.77 | 0.85 | 0.54 | 0 |
Step 2
The distance matrix below gives the current distance between clusters 1, 2, 3, and (4 & 5) using single linkage (the distance between 2 clusters is the maximum distance btwn any pair of penguins in the 2 clusters). By this, penguin 3 is closest to the cluster of penguins 4 & 5, with a distance of 0.85:
| 1 | 2 | 3 | 4 & 5 | |
|---|---|---|---|---|
| 1 | 0 | |||
| 2 | 0.94 | 0 | ||
| 3 | 2.19 | 2.60 | 0 | |
| 4 & 5 | 2.25 | 2.26 | 0.85 | 0 |
Step 3
The distance matrix below gives the current distance between clusters 1, 2, and (3, 4, 5) using single linkage. By this, clusters 1 and 2 are the closest, with a distance of 0.94:
| 1 | 2 | 3,4,5 | |
|---|---|---|---|
| 1 | 0 | ||
| 2 | 0.94 | 0 | |
| 3,4,5 | 2.19 | 2.26 | 0 |
Step 4
The distance matrix below gives the current distance between our 2 clusters, (1 & 2) and (3 & 4 & 5) using single linkage. The distance between them is 2.19 (hence the height of the final merge in our dendrogram):
| 1 & 2 | 3,4,5 | |
|---|---|---|
| 1 & 2 | 0 | |
| 3,4,5 | 2.19 | 0 |
EXAMPLE 4: Explore Clusters
Solution:
- too many. they’re very specific
- ….
- the clusters continue to merge as we go up the dendrogram. (eg: the 5-cluster solution is nested in the 4-cluster solution)
- yikes! this solution doesn’t capture the more natural looking clusters in the data. this algorithm is greedy – it makes the best decisions at each step, but the results aren’t necessarily globally optimal.
EXAMPLE 5: Details
Solution:
- Yes. See example 4.
- Clustering is a process of combining similar neighbors based on a full set of variables/features while KNN and Classifications look at points that are similar in terms of predictors with the goal of getting useful predictions of an outcome.
Exercises
Solutions will not be provided. These exercises are part of your homework this week.